


Quadratische Transformationen sind durch eine Modulgleichung vom Grad 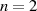 bestimmt,37
also durch Periodenverhältnisse wie z. B.
bestimmt,37
also durch Periodenverhältnisse wie z. B.
Die LANDEN-Transformation ist wahrscheinlich der bekannteste Vertreter aller quadratischen
Transformationen [AS72, 17.5], [WW27, §  ], [Ach70, § 38], [Cay76, § 254], [Tri48, IV, § 7],
[Hur00, II-7, § 5]. Sie ist gekennzeichnet durch die “Periodenbeziehungen”
], [Ach70, § 38], [Cay76, § 254], [Tri48, IV, § 7],
[Hur00, II-7, § 5]. Sie ist gekennzeichnet durch die “Periodenbeziehungen”
welche eine Teilung der ersten (also reellen) Periode durch zwei anzeigen.38
Transformationsbeziehung Die mit Gleichung 94 verbundenen Transformationsbeziehungen sind:39
Beweis. Beschränkt man sich auf die Periodenrechtecke um den Koordinatenursprung dann
liegen die Nullstellen von 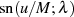 bekanntlich bei
bekanntlich bei 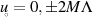 , was nach den
Periodenverhältnissen laut Gleichung 94 äquivalent zu
, was nach den
Periodenverhältnissen laut Gleichung 94 äquivalent zu 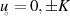 ist. Demzufolge liegen die
Nullstellen bezüglich
ist. Demzufolge liegen die
Nullstellen bezüglich  bei
bei 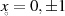 . In gleicher Art und Weise ergibt sich für die Pole
. In gleicher Art und Weise ergibt sich für die Pole
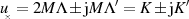 und entsprechend für
und entsprechend für 
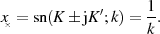
In Bezug auf den allgemeinen Lösungsansatzes muß es sich für 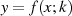 also um eine
Beziehung der Form
also um eine
Beziehung der Form
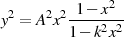 | (98) |
handeln. Um nun die Werte für den Multiplikator 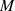 , das Modul
, das Modul 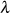 sowie
sowie 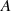 zu bestimmen ist es
günstig in beiden Lösungsansätzen das Verhältnis
zu bestimmen ist es
günstig in beiden Lösungsansätzen das Verhältnis 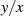 zu bilden und dann gleichzusetzen.
zu bilden und dann gleichzusetzen.
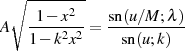 | (99) |
Setzt man nun noch die drei ausgewählten Werte 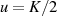 ,
, 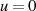 und
und 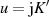 ein, dann sind die
(ebenfalls drei) Unbekannten leicht zu bestimmen. __
ein, dann sind die
(ebenfalls drei) Unbekannten leicht zu bestimmen. __
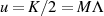 nimmt nach Gleichung 38 der elliptische Sinus (und demzufolge
auch
nimmt nach Gleichung 38 der elliptische Sinus (und demzufolge
auch  ) den Wert
) den Wert 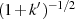 an und es gilt
an und es gilt
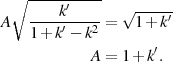
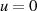 und folglich auch
und folglich auch 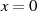 in Gleichung 99 ein, dann wird
wegen der Unbestimmtheit des rechtsseitigen Ausdrucks eine Grenzwertbestimmung nach
der Regel von BERNOULLI-L’HOSPITAL notwendig.
in Gleichung 99 ein, dann wird
wegen der Unbestimmtheit des rechtsseitigen Ausdrucks eine Grenzwertbestimmung nach
der Regel von BERNOULLI-L’HOSPITAL notwendig.
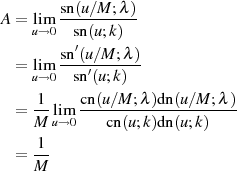
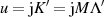 kann man beim rechtsseitigen Grenzübergang auf den
vorhergehenden Fall zurückführen, wenn
kann man beim rechtsseitigen Grenzübergang auf den
vorhergehenden Fall zurückführen, wenn 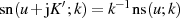 bzw.
bzw.
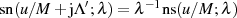 nach Tabelle 3 beachtet wird. Um auch den
linksseitigen Grenzwert ermitteln zu können, sind vorbereitend noch Zähler und Nenner
durch
nach Tabelle 3 beachtet wird. Um auch den
linksseitigen Grenzwert ermitteln zu können, sind vorbereitend noch Zähler und Nenner
durch  zu dividieren.
zu dividieren.
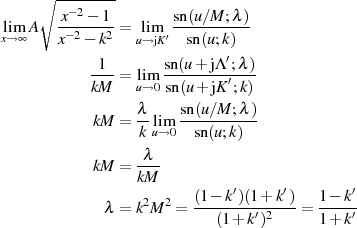
Eine weitere interessante Darstellung der Transformationsbeziehung ist möglich, wenn man die
Verschiebungsrelation 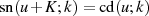 zu Hilfe nimmt.
zu Hilfe nimmt.
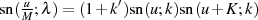
In äquivalenter Art und Weise kann auch die folgende Formel abgeleitet werden, wenn man die Periodenbeziehungen 94 der LANDEN-Transformation berücksichtigt.
![u u [ ′ ( K ) ( K )]2
sn(M-− Λ;λ)sn(M-+ Λ;λ )= − (1 + k)sn u+ -2;k sn u− 2-;k](elliptic793x.png)
Funktionsverlauf
Der Verlauf der Transformationsbeziehung 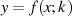 entsprechend Gleichung 98
entsprechend Gleichung 98
ist in Abbildung 10 grafisch dargestellt.
Im Gegensatz dazu zeigen die einzelnen Bilder in Abbildung 11 die äquivalente Parameterdarstellung
nach Gleichung 76 und 77. Der Parameter  läuft wieder auf dem Wegabschnitt
läuft wieder auf dem Wegabschnitt  in
Abbildung 8a von
in
Abbildung 8a von  nach
nach 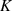 , dann auf dem Teilstück
, dann auf dem Teilstück  bis
bis 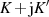 und zuletzt bis zum Punkt
und zuletzt bis zum Punkt
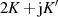 (bzw. rückwärts nach
(bzw. rückwärts nach 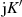 ).
).
Das Modul 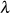 Um eine Vorstellung vom Verlauf der Modulgleichung
Um eine Vorstellung vom Verlauf der Modulgleichung 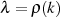 zu bekommen, wurde Formel 96 in Abbildung 12
grafisch dargestellt.40
zu bekommen, wurde Formel 96 in Abbildung 12
grafisch dargestellt.40
Aus der Modulbeziehung 96 können außerdem die folgenden nützlichen Vertauschungsrelationen abgeleitet werden.
Gebräuchliche Darstellungen für das Modul 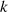 sind außerdem
sind außerdem
die wegen der Symmetrie von Formel 96 äquivalent auch für 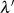 gelten.
gelten.
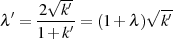 | (103) |
Eine weitere nützliche Formel für 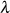 ist die folgende
ist die folgende
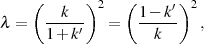
die sich aus der Multiplikation von Gleichung 96 mit 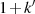 bzw.
bzw. 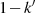 unter Berücksichtigung der
Definition des komplementären Moduls in Formel 1 ergibt.
unter Berücksichtigung der
Definition des komplementären Moduls in Formel 1 ergibt.
Beziehungen für  Die Transformationsbeziehung für
Die Transformationsbeziehung für 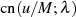 lautet
lautet
Beweis. Ausgangspunkt soll Definitionsgleichung 31 sowie die LANDEN-Transformation des
elliptischen Sinus’ in Formel 95 sein. Nach Kombination beider Gleichungen multipliziert man
zuerst alle Terme aus, extrahiert danach 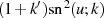 und vereinfacht abschließend durch
Anwendung des binomischen Satzes.
und vereinfacht abschließend durch
Anwendung des binomischen Satzes.
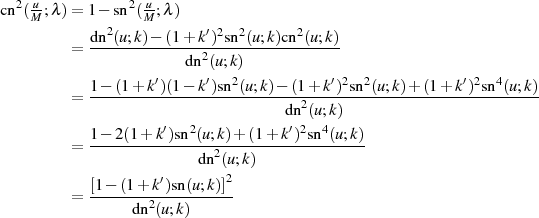
Beziehungen für 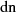 Die Beziehung für
Die Beziehung für 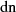 kann ebenfalls ausgehend von der des elliptischen Sinus’ in Gleichung 95 und
mit Hilfe seiner Definitionsgleichung 32 ermittelt werden.
kann ebenfalls ausgehend von der des elliptischen Sinus’ in Gleichung 95 und
mit Hilfe seiner Definitionsgleichung 32 ermittelt werden.
Beweis.
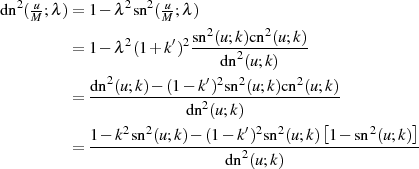
Ausmultiplizieren sowie nachfolgende Anwendung des Binomischen Satzes führt zu
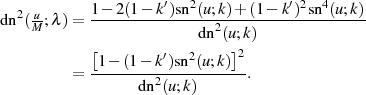
Die weitere Umformung der rechten Seite von Gleichung 105 kann jetzt noch so erfolgen, daß sie
einzig und allein auf 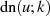 basiert.
basiert.
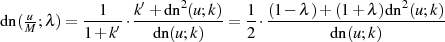
Trigonometrische Beziehungen Bezüglich Differentialgleichung 70 ist die LANDEN-Transformation durch die Substitution
gekennzeichnet. Mit der Beziehung für doppelte Winkel 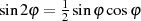 ist äquivalent
dazu
ist äquivalent
dazu
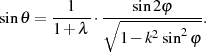
Aus Gleichung 104 ergibt sich folgerichtig für den Cosinus
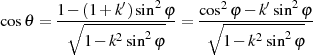 | (107) |
und mit dem Theorem 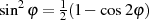 sowie der Modulbeziehung 96
sowie der Modulbeziehung 96
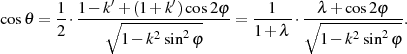
Insbesondere für numerische Berechnungen hat der trigonometrische Tangens Bedeutung. Die entsprechenden Beziehungen können direkt aus Formel 95 sowie 104 gewonnen werden.
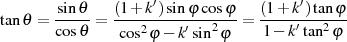 | (108) |
Eine weitere oft verwendete Darstellungsvariante auf der Grundlage des Tangens ist
Beweis. Ausmultiplizieren von Gleichung 108 gefolgt von Umstellen nach 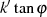 ergibt
ergibt
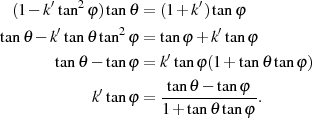
Mit dem Additionstheorem 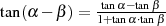 kann man nach
kann man nach 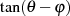 auflösen.
auflösen.
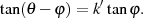
__
Eine ebenfalls oft zu findende Darstellung mit Hilfe des trigonometrischen Sinus’ lautet:
Beweis. Sie kann aus Gleichung 109 abgeleitet werden, wenn man die trigonometrische
Produktformel ![sinα cos β = 1∕2[sin(α+ β )+ sin(α − β)]](elliptic857x.png) anwendet.
anwendet.
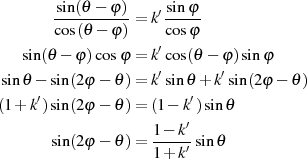
Beziehungen für 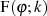 Aus den allgemeinen Transformationsbeziehungen 77 und 76 sowie Formel 97 resultiert sofort
folgende Darstellung
Aus den allgemeinen Transformationsbeziehungen 77 und 76 sowie Formel 97 resultiert sofort
folgende Darstellung
Die GAUSS-Transformation realisiert im Gegensatz zur LANDEN-Transformation (welche die reelle Periode teilt) eine Division der imaginären Periode durch zwei [Ach70, § 39], [Cay76, § 246]. Sie wird in vielen Literaturquellen durch folgende Gleichungen beschrieben.
Es ist nun relativ einfach die GAUSS-Transformation mit Hilfe der elliptischen Funktionen direkt aus der LANDEN-Transformation abzuleiten.41
Beweis. Nimmt man als Ausgangspunkt Gleichung 95 der LANDEN-Transformation und
ersetzt 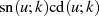 mit Hilfe von Gleichung 52, dann ergibt sich
mit Hilfe von Gleichung 52, dann ergibt sich
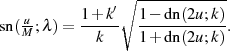
Quadrieren und Umstellen nach 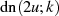 führt zu einer ersten recht bekannten Gleichung der
GAUSS-Transformation.
führt zu einer ersten recht bekannten Gleichung der
GAUSS-Transformation.
Will man die Beziehungen für den elliptischen Sinus ermitteln, dann ist auf der linken Seite noch
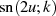 zu extrahieren. Dazu verwendet man am am einfachsten Definitionsgleichung 32 der
Delta-Amplitude sowie Hilfsformel 102.
zu extrahieren. Dazu verwendet man am am einfachsten Definitionsgleichung 32 der
Delta-Amplitude sowie Hilfsformel 102.
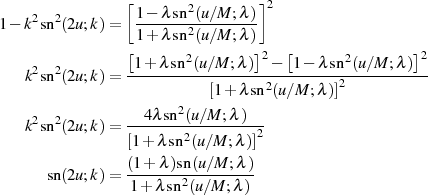
Nimmt man zuletzt noch die Ersetzungen
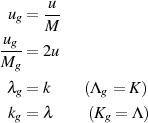
vor und bezieht die Transformationsbeziehungen 95, 97, und 96 mit ein, dann erhält man die Beziehungen der GAUSS-Transformation.42
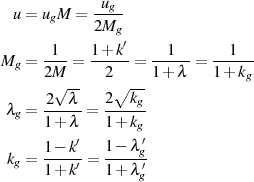
Beziehungen für 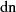 Für die Delta-Amplitude
Für die Delta-Amplitude 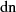 ergibt sich die Transformationsbeziehung recht einfach aus
Zwischenformel 116, wenn Gleichung 34 in der Form
ergibt sich die Transformationsbeziehung recht einfach aus
Zwischenformel 116, wenn Gleichung 34 in der Form
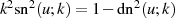
berücksichtigt wird.
Beziehungen für  Die noch ausstehende Beziehung für
Die noch ausstehende Beziehung für  lautet
lautet
Trigonometrische Beziehungen Die gesuchte Beziehung für den Sinus erhält man wieder durch direkte Umsetzung von Transformationsbeziehung 113 mit Hilfe der trigonometrischen Äquivalenzen in Gleichung 70 sowie 30.
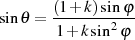
Eine eng mit der GAUSS-Form des elliptischen Integrals erster Art (siehe Gleichung 6) verbundene Darstellung ist immer die über den Tangens. Sie kann aus der vorangegangenen Gleichung sowie dem Äquivalent für den Cosinus nach Formel 118
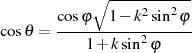
gewonnen werden, wenn man dann noch die trigonometrische Beziehung 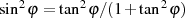 hinzuzieht.
hinzuzieht.
Periodenverhältnis Die Bestimmung des Periodenverhältnisses gestaltet sich ausgehend von den Periodenbeziehungen der LANDEN-Transformation relativ einfach. Man muß dabei nur Gleichung 94 auf die mit einem tiefgestellten “g” gekennzeichneten Größen der GAUSS-Transformation umsetzen.