


Eine auf elliptischen Funktionen basierende Lösung der Differentialgleichung 70 ist
ermittelbar, wenn man zu einer Parameterdarstellung mit Hilfe der neuen Variablen  übergeht.28
übergeht.28
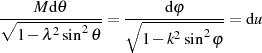
Integriert man nun beide Seiten und nimmt die Definitionsgleichung 29 der Amplitudenfunktion des
elliptischen Sinus’ (Gleichung 30) hinzu, so ergibt sich für 
In Gleichung 76 wurde auf die Einführung einer Integrationskonstante verzichtet, da man ohne
wesentliche Einschränkung vom Funktionswert 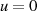 für
für 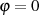 ausgehen kann.
ausgehen kann.
Für 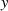 erhält man in gleicher Art und Weise
erhält man in gleicher Art und Weise
wobei diesmal eine Integrationskonstante 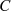 berücksichtigt werden muß.
berücksichtigt werden muß.
Fragt man sich nun, welche Werte der Parameter  grundsätzlich annehmen darf, damit
grundsätzlich annehmen darf, damit  reell wird, dann ist ein Blick auf Abbildung 8 hilfreich. Sie zeigt nocheinmal den Verlauf
von
reell wird, dann ist ein Blick auf Abbildung 8 hilfreich. Sie zeigt nocheinmal den Verlauf
von 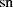 für komplexe Argumente, wobei die zusätzlichen Parameterlinien anschaulich
illustrieren,29
daß
für komplexe Argumente, wobei die zusätzlichen Parameterlinien anschaulich
illustrieren,29
daß  nur entlang der Geraden
nur entlang der Geraden 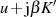 für reelles
für reelles  und
und 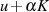 für imaginäres
für imaginäres  nicht komplex
ist (
nicht komplex
ist (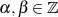 ).
).
Mit diesem Wissen kann man bezüglich  den mit Pfeilen markierten “Wertepfad” in Abbildung 8a
für das Argument
den mit Pfeilen markierten “Wertepfad” in Abbildung 8a
für das Argument  angeben. Dieser Weg garantiert zwar, daß
angeben. Dieser Weg garantiert zwar, daß  monoton Werte zwischen
monoton Werte zwischen 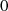 und
und  annimmt, jedoch sind weitere
annimmt, jedoch sind weitere  -Werte möglich, wenn man die Periodizität des elliptischen Sinus’
berücksichtigt.
-Werte möglich, wenn man die Periodizität des elliptischen Sinus’
berücksichtigt.
Soll auch 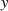 (oder zumindest
(oder zumindest 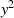 ) reell sein,30
dann muß sich
) reell sein,30
dann muß sich  auf dem Gitter
auf dem Gitter 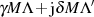 (
(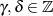 ) bewegen. Abbildung 9 illustriert dieses
anschaulich, wobei folgende Definitionen für die reelle bzw. imaginäre Periode von
) bewegen. Abbildung 9 illustriert dieses
anschaulich, wobei folgende Definitionen für die reelle bzw. imaginäre Periode von  und
und 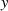 gelten
sollen:31
gelten
sollen:31

Sinnvolle Werte für die Integrationskonstante 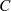 sind entsprechend nur
sind entsprechend nur 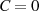 und
und  , wobei der Wert
, wobei der Wert 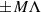 rein reelle Werte für
rein reelle Werte für 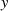 bei geradem
bei geradem 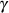 ermöglicht.32
Auf der Grundlage dieser Betrachtungen, welche ja im Wesen auf der doppelten Periodizität des elliptischen
Sinus’ basieren, kann man (ohne etwas zu verändern) die Gleichungen 76 und 77 auch folgendermaßen
schreiben:33
ermöglicht.32
Auf der Grundlage dieser Betrachtungen, welche ja im Wesen auf der doppelten Periodizität des elliptischen
Sinus’ basieren, kann man (ohne etwas zu verändern) die Gleichungen 76 und 77 auch folgendermaßen
schreiben:33
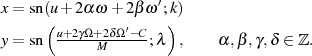
Soll gewährleistet sein, daß nur eine endliche Anzahl möglicher
(unterschiedlicher)  -Werte zu einem bestimmten Wert
-Werte zu einem bestimmten Wert 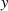 gehören (sowie
umgekehrt),34
dann muß man ausgehend von diesen Gleichungen die Periodenbedingung
gehören (sowie
umgekehrt),34
dann muß man ausgehend von diesen Gleichungen die Periodenbedingung
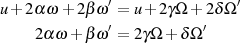
formulieren. Separiert man darin Real- und Imaginärteil, dann ergibt sich für den Fall eines reellen
Multiplikators 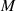
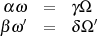 | (78) |
und im einfachsten Fall, d. h. wenn 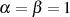 gilt
gilt
Für den Fall eines ganzzahligen Verhältnisses 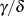 bzw.
bzw. 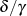 , also eines Periodenverhältnisses der
Form
, also eines Periodenverhältnisses der
Form
spricht man bezüglich der Beziehung zwischen 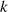 und
und 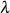 von einer Modulgleichung vom Grad
von einer Modulgleichung vom Grad
 .
.
Der Spezialfall 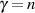 ,
, 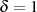 wird dabei als die 1. elliptische Haupttransformation (
wird dabei als die 1. elliptische Haupttransformation ( -te Teilung der
reellen Periode), der Fall
-te Teilung der
reellen Periode), der Fall 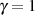 ,
, 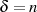 als 2. elliptische Haupttransformation (
als 2. elliptische Haupttransformation ( -te Teilung der
imaginären Periode) bezeichnet.
-te Teilung der
imaginären Periode) bezeichnet.