


LEGENDRE’sche Normalform Das unvollständige elliptische Integral erster Art ist in seiner LEGENDRE-Form folgendermaßen definiert
wobei mit 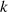 das Modul und
das Modul und  die Amplitude bezeichnet wird.
die Amplitude bezeichnet wird.
JACOBI-Form
Mit der Substitution 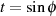 in Gleichung 3 gelangt man zu der von C.G.J. JACOBI bevorzugten
Form.
in Gleichung 3 gelangt man zu der von C.G.J. JACOBI bevorzugten
Form.
Beweis.
Einsetzen der Substitution sowie der Ableitung 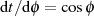 in Definitionsgleichung 3 führt
sofort zum Ergebnis
in Definitionsgleichung 3 führt
sofort zum Ergebnis
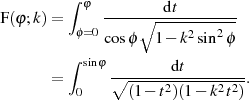
Um im weiteren die Eindeutigkeit zu gewährleisten und außerdem eine einfache Schreibweise des
Integrals bei Verwendung des Argumentes  zu erhalten, soll außerdem definiert sein:
zu erhalten, soll außerdem definiert sein:
RIEMANN’sche Normalform
Eine weitere, heute nicht mehr so geläufige Form, ist die RIEMANN’sche Form. Sie kommt zustande,
wenn man in der JACOBI’schen Darstellung nach Gleichung 5 den Term 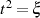 substituiert. Mit dem
zugehörigen Differential
substituiert. Mit dem
zugehörigen Differential  ergibt sich so
ergibt sich so
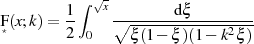
und letztlich (die nicht besonders gekennzeichnete) RIEMANN’sche Normalform des Integrals.
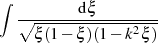
GAUSS-Form Eine von C.F. GAUSS intensiv verwendete Form des elliptischen Integrals erster Art4 ist
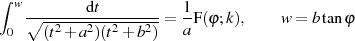 | (6) |
mit dem Modul
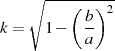 | (7) |
sowie dem komplementären Modul (konform zu Definitionsgleichung 1)
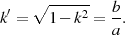 | (8) |
Beweis. Um dieses Integral auf 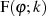 zurückzuführen, wird zuerst eine passende Substitution
nach [AS72, 17.4.41 ff.] gewählt
zurückzuführen, wird zuerst eine passende Substitution
nach [AS72, 17.4.41 ff.] gewählt
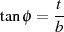 | (9) |
und dann mit Hilfe von 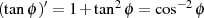 die Ableitung
die Ableitung 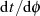 gebildet.
gebildet.
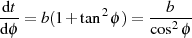
Einsetzen in das Ausgangsintegral ergibt
Vergleich mit Formel 3 zeigt, daß es sich hier um das unbestimmte elliptische Integral erster Art 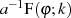 handelt.5
handelt.5
LEGENDRE’sche Normalform mit Modulwinkel
Manchmal wird das elliptische Integral erster Art auch über den sogenannten Modulwinkel  , mit
, mit  ,
angegeben.6
,
angegeben.6
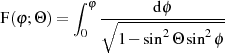
Der Funktionswert für 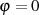 ist trivial und direkt aus Definitionsgleichung 3 ersichtlich.
ist trivial und direkt aus Definitionsgleichung 3 ersichtlich.
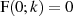
Für  entartet die Funktion zum vollständigen elliptischen Integral erster Art
entartet die Funktion zum vollständigen elliptischen Integral erster Art  , wobei
, wobei 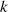 dann die Rolle des Arguments übernimmt (vgl. Abschnitt 2.2).
dann die Rolle des Arguments übernimmt (vgl. Abschnitt 2.2).
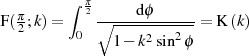 | (11) |
Der Funktionswert bei 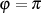 ergibt sich auf dieser Grundlage zu
ergibt sich auf dieser Grundlage zu  .
.
Beweis.
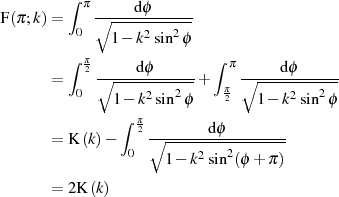
Für spezielle Module sind geschlossene Lösungen des Integrals möglich.
Zuerst sei auf Abbildung 1 verwiesen, die 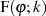 im Intervall
im Intervall 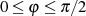 darstellt. Relativ leicht
nachzuweisen ist, daß
darstellt. Relativ leicht
nachzuweisen ist, daß 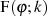 eine ungerade Funktion ist.
eine ungerade Funktion ist.
Beweis. Mit der Substitution 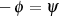 in der Definitionsgleichung des Integrals kann man
schnell beweisen, daß
in der Definitionsgleichung des Integrals kann man
schnell beweisen, daß 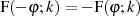 gilt.
gilt.
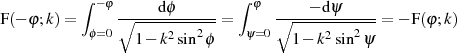
__
 ist für alle
ist für alle  eine monoton steigende Funktion. Die Begründung liegt in Gleichung 16, der
ersten Ableitung von
eine monoton steigende Funktion. Die Begründung liegt in Gleichung 16, der
ersten Ableitung von 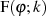 . Für kleine Werte
. Für kleine Werte  gilt
gilt 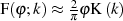 , was sich direkt aus
Abbildung 1 ablesen läßt, wenn man außerdem Gleichung 11 berücksichtigt.
, was sich direkt aus
Abbildung 1 ablesen läßt, wenn man außerdem Gleichung 11 berücksichtigt.
Eine besondere Bedeutung im Zusammenhang mit den elliptischen Funktionen (Abschnitt 3) hat folgende Relation, die auch in Abbildung 2 erkennbar ist.
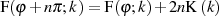 | (14) |
Außerdem ist Gleichung 14 eine logische Schlußfolgerung, wenn man wie gewohnt das Integral als
Fläche unter der periodischen Kurve 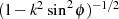 interpretiert (vgl. Abbildung 3).
interpretiert (vgl. Abbildung 3).
Aus der zweiten Ableitung nach Gleichung 17 und dem Funktionsverlauf entsprechend Abbildung 2
ist ersichtlich, daß die Wendepunkte bei 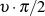 mit
mit 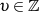 liegen.
liegen.
Das Differential von 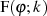 ist nach dem Hauptsatz der Differential- und
Integralrechnung7
ist nach dem Hauptsatz der Differential- und
Integralrechnung7
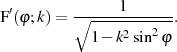 | (16) |
Nochmaliges Differenzieren der ersten Ableitung 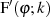 ergibt
ergibt
Für imaginäre Argumente entartet das unvollständige elliptische Integral zu
Beweis. Einsetzen des imaginären Arguments im Sinne von 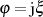 in Definitionsgleichung 3
führt zu
in Definitionsgleichung 3
führt zu
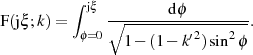
Mit der (im Intervall 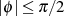 ) eindeutigen Substitution
) eindeutigen Substitution
 | (19) |
und deren Ableitung 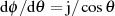 kann man das Differential
kann man das Differential
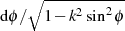 relativ einfach mit Hilfe des komplementären Moduls
relativ einfach mit Hilfe des komplementären Moduls 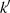 ausdrücken.8
ausdrücken.8
Schreibt man die rechte Seite von Gleichung 18 mit Hilfe der GUDERMANN-Funktion
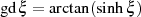 , dann gilt entsprechend:
, dann gilt entsprechend:
