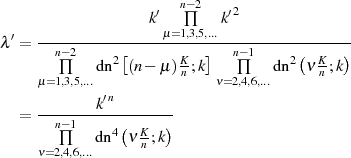Charakteristisch für die 1. elliptische Haupttransformation ist, daß die reelle Periode
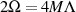 von
von  genau
genau  -mal die reelle Periode
-mal die reelle Periode 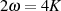 von
von
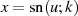 teilt, die imaginären Perioden aber gleich sind (
teilt, die imaginären Perioden aber gleich sind ( -te Teilung der ersten
Periode,43
vgl. Fall
-te Teilung der ersten
Periode,43
vgl. Fall  ,
,  in Abschnitt 4.5).
in Abschnitt 4.5).
Das sich ergebende Periodenverhältnis
zeigt, daß es sich bei der Beziehung zwischen 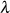 und
und 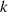 um eine Modulgleichung vom Grad
um eine Modulgleichung vom Grad  handelt.44
handelt.44
Den Verlauf für  und
und 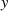 im Bereich
im Bereich  in Abhängigkeit vom Parameter
in Abhängigkeit vom Parameter  zeigt
Abbildung 13.
zeigt
Abbildung 13.
Für ungerades 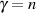 muß die Integrationskonstante
muß die Integrationskonstante 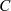 aus Abschnitt 4.5
verschwinden, damit
aus Abschnitt 4.5
verschwinden, damit  auf Wegabschnitt
auf Wegabschnitt 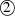 in Abbildung 8a reell
ist.45
in Abbildung 8a reell
ist.45
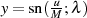 | (124) |
Der zugeordnete Verlauf des Parameters  ist für diesen Fall nocheinmal anschaulich in Abbildung 14
illustriert (inklusive der positiven Nullstellen und Pole), wobei fett dargestellte Gitternetzlinien reelle
Werte des elliptischen Sinus’ kennzeichnen.
ist für diesen Fall nocheinmal anschaulich in Abbildung 14
illustriert (inklusive der positiven Nullstellen und Pole), wobei fett dargestellte Gitternetzlinien reelle
Werte des elliptischen Sinus’ kennzeichnen.
Der Funktionsverlauf von 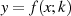 ist in Abbildung 15 dargestellt.
ist in Abbildung 15 dargestellt.
Er ist direkt aus dem Gitter in Abbildung 14 erklärbar, wenn man folgendes bedenkt:
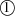 läuft
läuft  von
von 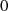 nach
nach 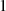 (
( entsprechend von
entsprechend von 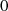 bis
bis 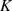 ), während
), während
 wegen Gleichung 121 genau
wegen Gleichung 121 genau  -mal die reelle Viertelperiode des elliptischen Sinus
durchläuft und dadurch
-mal die reelle Viertelperiode des elliptischen Sinus
durchläuft und dadurch 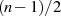 Nullstellen erzeugt.46
Nullstellen erzeugt.46
 läuft
läuft  von
von 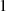 bis
bis 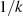 (siehe auch Tabelle 5). Da die imaginären
(Halb-) Perioden von
(siehe auch Tabelle 5). Da die imaginären
(Halb-) Perioden von  und
und 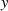 nach Formel 122 aber gleich sind, bewegt sich
nach Formel 122 aber gleich sind, bewegt sich  äquivalent von
äquivalent von 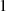 bis
bis 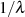 .
.
 des Weges von
des Weges von  herrschen ähnliche Verhältnis wie auf dem Ersten,
nur daß
herrschen ähnliche Verhältnis wie auf dem Ersten,
nur daß 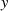 hier invertiert ist und so wegen Formel 121 genau
hier invertiert ist und so wegen Formel 121 genau 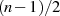 Pole generiert.
Pole generiert.Aus den wichtigsten Eigenschaften der Differentialgleichung 70 sowie der Transformationsfunktion, welche in Abschnitt 4.5 erarbeitet wurden, hat schon C.G.J. JACOBI in [Jac29] die folgende spezielle Form der rationalen Transformationsfunktion geschlußfolgert (vgl. auch [Cay76, § 229], [Ach70, § 40]).
Sie gewährleistet insbesondere, daß
 eine rationale, ungerade Polynomfunktion der Form
eine rationale, ungerade Polynomfunktion der Form 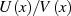 ist;
ist;
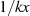 konform zu Gleichung 81 erfüllt
werden kann;
konform zu Gleichung 81 erfüllt
werden kann;
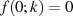 und
und 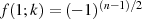 realisierbar sind.47
realisierbar sind.47
Offen ist unter anderem die Bestimmung der Koeffizienten  , welche sowohl zur Berechnung von
, welche sowohl zur Berechnung von 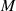 als auch
als auch 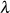 benötigt werden. Dazu muß man sich über die Lage und Anzahl der Nullstellen in
Gleichung 125 klar werden.
benötigt werden. Dazu muß man sich über die Lage und Anzahl der Nullstellen in
Gleichung 125 klar werden.
 Nullstellen, wobei
Nullstellen, wobei  davon letztlich die Koeffizienten
davon letztlich die Koeffizienten 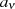 erzeugen.
erzeugen.
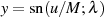 ,
müssen diese Nullstellen ebenfalls enthalten sein.
,
müssen diese Nullstellen ebenfalls enthalten sein.Die Koeffizienten 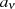 der rationalen Transformationsgleichung 125 sind nun folgendermaßen
bestimmt
der rationalen Transformationsgleichung 125 sind nun folgendermaßen
bestimmt
Beweis. Kennt man die Nullstellen 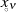 von Gleichung 125, dann kennt man auch die Koeffizienten
von Gleichung 125, dann kennt man auch die Koeffizienten
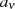 darin.48
darin.48
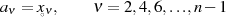
Die reellen Nullstellen, die alle im Bereich 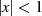 bzw.
bzw. 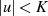 liegen, ergeben sich aus der
elliptischen Parameterdarstellung für
liegen, ergeben sich aus der
elliptischen Parameterdarstellung für 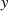
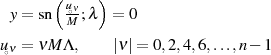
sowie der für  in Verbindung mit den Periodenbeziehungen.
in Verbindung mit den Periodenbeziehungen.
Die 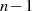 reellen Pole ermitteln sich nun recht einfach, wenn man in Gleichung 125 die Produktterme
des Nenners Null setzt.
reellen Pole ermitteln sich nun recht einfach, wenn man in Gleichung 125 die Produktterme
des Nenners Null setzt.
Zum gleichen Ergebnis gelangt man, wenn die elliptische Darstellung mittels Gleichung 76 und 77 als
Ausgangspunkt genommen wird. Die Pole liegen dann offensichtlich auf dem Wegabschnitt  laut
Abbildung 14 bzw. Tabelle 5, und zwar bei
laut
Abbildung 14 bzw. Tabelle 5, und zwar bei 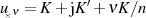 .
.
Die lokalen Extremwerte, deutlich sichtbar auch in Abbildung 15, liegen bei
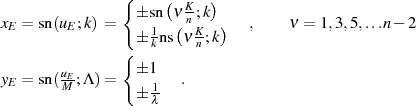
Beweis. Die Bestimmung der Extremwerte kann (wie üblich) mit Hilfe der ersten
Ableitung von  erfolgen. Bedenkt man aber, daß
erfolgen. Bedenkt man aber, daß  ja die Lösung der
Differentialgleichung 69 ist, dann kann man mit Blick auf Formel 71 sofort zur Bestimmung
der Nullstellen von
ja die Lösung der
Differentialgleichung 69 ist, dann kann man mit Blick auf Formel 71 sofort zur Bestimmung
der Nullstellen von 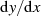 übergehen.
übergehen.
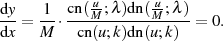
Die Kombination der Nullstellen von 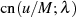 und
und 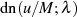 führt nach Tabelle 1 für
führt nach Tabelle 1 für
 zu den Extremstellen
zu den Extremstellen
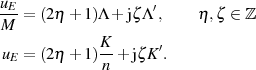
Berücksichtigt man die Ausprägungen des elliptischen Sinus’ für spezielle Argumente nach Tabelle 2, dann kann der Beweis abgeschlossen werden.
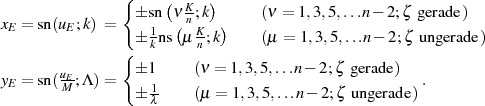
Transformationsbeziehung für 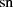 Die Transformationsbeziehung bei Verwendung des elliptischen Sinus’ ist direkt in Gleichung 125
enthalten, wenn man
Die Transformationsbeziehung bei Verwendung des elliptischen Sinus’ ist direkt in Gleichung 125
enthalten, wenn man  und
und 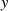 entsprechend der Beziehungen 76 und 77 ersetzt.
entsprechend der Beziehungen 76 und 77 ersetzt.
Aus der letzten Darstellung der Transformationsbeziehung läßt sich auch die Linearfaktorzerlegung mit Hilfe der Pol- und Nullstellen gewinnen.

Weitere interessante Darstellungen der Transformationsbeziehung 129 ergeben sich bei Vorwegnahme von Gleichung 138
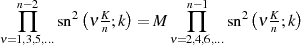
sowie Multiplikationsformel 47.

Transformationsbeziehung für  Die Beziehungen für
Die Beziehungen für  und
und 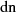 können z. B. abgeleitet werden, indem man die Pole und Nullstellen
der (ebenfalls) rationalen Polynome
können z. B. abgeleitet werden, indem man die Pole und Nullstellen
der (ebenfalls) rationalen Polynome 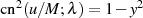 und
und 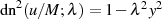 ermittelt.
Beide Funktionen haben die gleichen Pole, wie der elliptische Sinus
ermittelt.
Beide Funktionen haben die gleichen Pole, wie der elliptische Sinus 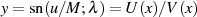 für
diesen Fall.
für
diesen Fall.
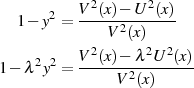
Zur Bestimmung der Linearfaktoren des Zählers wird zuerst der elliptische Cosinus 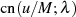 betrachtet, dessen Nullstellen bei
betrachtet, dessen Nullstellen bei 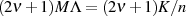 mit
mit  liegen. An diesen Stellen
nimmt
liegen. An diesen Stellen
nimmt  nach Gleichung 76 die Werte
nach Gleichung 76 die Werte ![sn[(2ν+ 1)K ∕n;k]](elliptic1006x.png) an. Da der Grad des Zählerpolynoms
genau dem von
an. Da der Grad des Zählerpolynoms
genau dem von 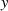 entspricht läßt sich folgende Linearfaktordarstellung angeben, die abgesehen vom
Vorfaktor
entspricht läßt sich folgende Linearfaktordarstellung angeben, die abgesehen vom
Vorfaktor 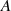 eindeutig bestimmt ist.
eindeutig bestimmt ist.
![4n−1 [ ( K- )]
μ=∏1,3,5,... x− sn μ n;k
1− y2 = cn2(Mu;λ)= A2--n−1--[--------(----)--]--
∏ 1− k2sn2 νKn-;k x22
ν=2,4,6,...](elliptic1009x.png)
Wegen der Symmetrie 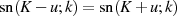 und der Spiegelungsbeziehung
und der Spiegelungsbeziehung
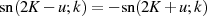 kann man den Zähler vereinfachen.
kann man den Zähler vereinfachen.
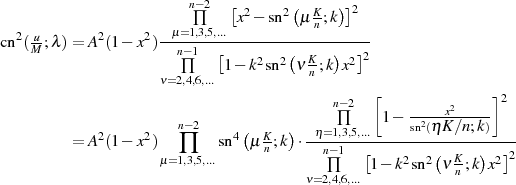
Aus dem schon bekannten Funktionswert  entsprechend Abschnitt 4.5, Formel 82
kann man abschließend den Vorfaktor
entsprechend Abschnitt 4.5, Formel 82
kann man abschließend den Vorfaktor  ermitteln
ermitteln
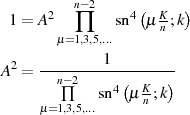
und damit die Transformationsbeziehung für  angeben.
angeben.
Transformationsbeziehung für 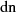 Für
Für 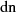 kann man in gleicher Art und Weise verfahren, also beginnend mit der Bestimmung der
Nullstellen. Wegen
kann man in gleicher Art und Weise verfahren, also beginnend mit der Bestimmung der
Nullstellen. Wegen  nach Tabelle 3 liegen die Nullstellen (bezüglich
nach Tabelle 3 liegen die Nullstellen (bezüglich  ) bei
) bei
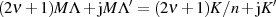 mit
mit 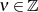 . Da aber (vgl. ebenfalls Tabelle 3) für
. Da aber (vgl. ebenfalls Tabelle 3) für 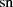 die Beziehung
die Beziehung 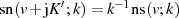 gilt, nimmt
gilt, nimmt  an den Nullstellen die Werte
an den Nullstellen die Werte
![k−1ns [(2ν +1 )K ∕n;k]](elliptic1027x.png) an. Nun ist man (wie beim elliptischen Cosinus auch) in der Lage eine
entsprechende Linearfaktordarstellung anzugeben.
an. Nun ist man (wie beim elliptischen Cosinus auch) in der Lage eine
entsprechende Linearfaktordarstellung anzugeben.
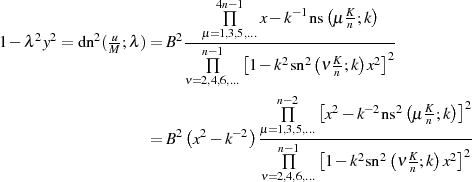
Aus dem Funktionswert 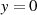 an der Stelle
an der Stelle 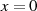 kann man wieder den Vorfaktor bestimmen.
kann man wieder den Vorfaktor bestimmen.
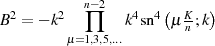
Einsetzen und Ausmultiplizieren des Zählers liefert das Ergebnis
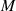
Mit dem Funktionswert 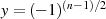 an der Stelle
an der Stelle 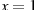 kann man den Multiplikator
kann man den Multiplikator 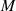 in
Gleichung 125 recht einfach bestimmen (vgl. auch allgemeine Aussagen in Abschnitt 4.5,
Formel 82).
in
Gleichung 125 recht einfach bestimmen (vgl. auch allgemeine Aussagen in Abschnitt 4.5,
Formel 82).
Mit der Formel für die Koeffizienten 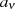 ergeben sich neue Darstellungsmöglichkeiten sowohl für
ergeben sich neue Darstellungsmöglichkeiten sowohl für 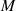 als auch
als auch 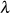 . Dazu soll mit Hilfe der Verschiebungsrelation
. Dazu soll mit Hilfe der Verschiebungsrelation 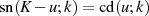 nach 3 zuerst der
folgende (mehrfach auftretende) Term vereinfacht werden.
nach 3 zuerst der
folgende (mehrfach auftretende) Term vereinfacht werden.
Jetzt kann ausgehend von Gleichung 133 der Multiplikator 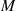 konkretisiert werden.
konkretisiert werden.
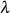
Aus der Eigenschaft der Unveränderlichkeit von Differentialgleichung 69 für 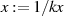 und
und
 nach Formel 81 kann man das Modul
nach Formel 81 kann man das Modul 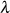 ermitteln.
ermitteln.
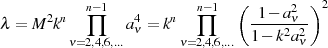 | (136) |
Beweis. Dazu geht man wieder von Gleichung 125 aus und nimmt darin die entsprechenden Substitutionen vor.
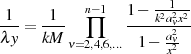
Da auch hier die Bedingung 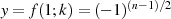 erfüllt sein soll (vgl. spezielle Werte
nach Formel 82), kann man, wenn Gleichung 133 hinzugenommen wird, schreiben
erfüllt sein soll (vgl. spezielle Werte
nach Formel 82), kann man, wenn Gleichung 133 hinzugenommen wird, schreiben
Setzt man nun die Darstellung für 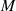 nach Formel 135 in Gleichung 137 ein, dann erhält man recht
schnell eine Darstellung für
nach Formel 135 in Gleichung 137 ein, dann erhält man recht
schnell eine Darstellung für  , die nur noch von den Koeffizienten
, die nur noch von den Koeffizienten 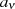 abhängt. Dazu werden Zähler
und Nenner außerdem mit mit
abhängt. Dazu werden Zähler
und Nenner außerdem mit mit 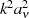 multipliziert und dann mittels
multipliziert und dann mittels 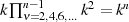 weiter
vereinfacht.
weiter
vereinfacht.

Wie auch in [Jac29, § 23] dargestellt, führt (unter Zuhilfenahme von Formel 134) Einsetzen der
Koeffizientenbeziehung 126 zu der folgenden bekannten Form für 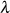 :
:
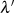
Die Beziehung zwischen den komplementären Modulen kann direkt aus Gleichung 132 abgelesen
werden, wenn man dort den speziellen Wert  (also
(also 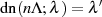 ) einsetzt.
) einsetzt.
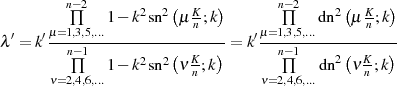
Mit 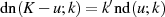 kann man diese Relation bei entsprechender Umindizierung sogar noch
weiter vereinfachen.
kann man diese Relation bei entsprechender Umindizierung sogar noch
weiter vereinfachen.