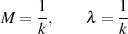Eine tabellarische Übersicht der Transformationen erster Ordnung sowie der geeigneten Substitutionen ist unter anderem in [Tri48, lV, § 2] zu finden. Wir beschränken uns hier auf zwei wichtige Transformationen – JACOBI’s reelle sowie imaginäre Transformation.
Die imaginäre Transformation wurde in Bezug auf das elliptische Integral erster Art schon in
Abschnitt 2.1, für den elliptischen Sinus in Abschnitt 3.10 behandelt. Um die Parameter 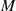 und
und 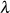 aus der allgemeinen Gleichung 70 zu ermitteln, ist ein Blick auf Beziehung 18 notwendig.
aus der allgemeinen Gleichung 70 zu ermitteln, ist ein Blick auf Beziehung 18 notwendig.
![F (φ; k)= jF[arctan(sinhjφ);k′]](elliptic735x.png)
Diese Gleichung ist nun der folgenden speziellen Ausprägung von Differentialgleichung 70
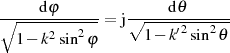 | (87) |
mit der Substitution nach Gleichung 19
äquivalent. Aus der spezifischen Beziehung 87 kann man durch Vergleich mit Differentialgleichung 70 sofort den Multiplikator und die zugeordnete Modulgleichung (vom Grad Eins) ablesen.
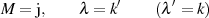
Die Bestimmung des Periodenverhältnisses ist mit diesen Werten kein Problem mehr.
Die rationale Beziehung zwischen  und
und 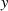 ist schon in der Substitution 19 enthalten, wenn man (wie
immer) Gleichung 76 sowie 77 berücksichtigt.
ist schon in der Substitution 19 enthalten, wenn man (wie
immer) Gleichung 76 sowie 77 berücksichtigt.
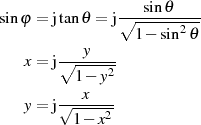
JACOBI’s reelle Transformation nach folgender Gleichung
ermöglicht es, bei allen elliptischen Funktionen auch Module 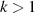 zuzulassen.
zuzulassen.
Beweis. Ausgehend vom Argument des Integrals 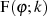
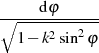
nimmt man die Substitution 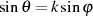 , welche ja eine algebraische Beziehung erster
Ordnung, nämlich
, welche ja eine algebraische Beziehung erster
Ordnung, nämlich 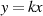 verkörpert, vor. Mit der Ableitung
verkörpert, vor. Mit der Ableitung 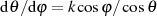 erhält
man wieder die typische Differentialgleichung
erhält
man wieder die typische Differentialgleichung
aus welcher nur noch die Parameter 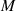 und
und 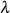 konform zu Gleichung 70 abgelesen werden
müssen. __
konform zu Gleichung 70 abgelesen werden
müssen. __