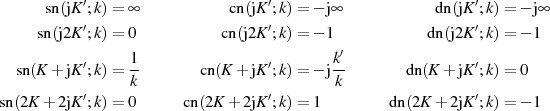In diesem Abschnitt sollen noch einige Formeln für den Übergang auf andere Argumente genannt (und teilweise auch abgeleitet) werden. Eine komprimierte Übersicht zu den interessanten Fällen enthält Tabelle 3, eine vollständige Tabellierung für alle elliptischen Funktionen ist in [AS72, 16.8] zu finden.
Alle Formeln in Tabelle 3 ergeben sich direkt aus den Additionstheoremen 40, 45 und 46 sowie den
Gleichungen für komplexe Argumente, wenn man jeweils die um 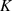 bzw.
bzw. 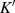 verschobenen
Argumente betrachtet. Aus den Beziehungen in Tabelle 3 für die gilt
verschobenen
Argumente betrachtet. Aus den Beziehungen in Tabelle 3 für die gilt 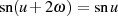 (beispielhaft
für
(beispielhaft
für 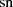 ), ist sofort die reelle, imaginäre und komplexe Periode der elliptischen Basisfunktionen
ersichtlich (siehe Tabelle 4 sowie Abbildungen 6 und 7).
), ist sofort die reelle, imaginäre und komplexe Periode der elliptischen Basisfunktionen
ersichtlich (siehe Tabelle 4 sowie Abbildungen 6 und 7).
| Reelle | Imaginäre | Komplexe | |
| Funktion | Periode
| ||
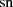 | 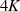 | 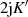 | 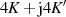 |
 | 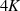 | 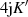 | 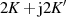 |
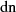 | 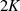 | 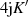 | 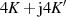 |
Folgende spezielle (komplexe) Werte ergeben sich außerdem aus verschiedenen Fällen in Tabelle 3.