


Konsequent kann man auch die Definition des Erwartungswertes einer  -dimensionalen Zufallsgröße
aus dem der eindimensionalen Größe ableiten, wenn man außerdem Gleichung 17 bzw. den Ideenkreis
um sie herum, berücksichtigt [Gne58, § 25 ff.].
-dimensionalen Zufallsgröße
aus dem der eindimensionalen Größe ableiten, wenn man außerdem Gleichung 17 bzw. den Ideenkreis
um sie herum, berücksichtigt [Gne58, § 25 ff.].
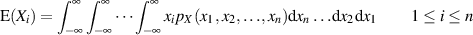
Man muß allerdings hinzufügen, daß es sich um den Erwartungswert der Randverteilung für 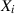 handelt. Praktisch ergibt sich dadurch ein Erwartungswerte-Vektor.
handelt. Praktisch ergibt sich dadurch ein Erwartungswerte-Vektor.
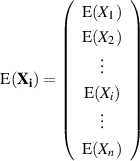
Die Varianz(en) einer  -dimensionalen Zufallsgröße können aus der allgemeinen Definitionsgleichung 2
in Verbindung mit dem Erwartungswert (von eben) ermittelt werden.
-dimensionalen Zufallsgröße können aus der allgemeinen Definitionsgleichung 2
in Verbindung mit dem Erwartungswert (von eben) ermittelt werden.
![Var(Xi)= E[Xi− E(Xi)]2 1 ≤ i≤ n](probabil183x.png)
Auch hier muß man hinzufügen, daß es sich um die Varianz einer Randverteilung handelt.
Sind 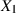 und
und 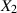 zwei (nicht notwendigerweise unabhängige) Zufallsgrößen, dann nennt man die
folgende Größe Kovarianz von
zwei (nicht notwendigerweise unabhängige) Zufallsgrößen, dann nennt man die
folgende Größe Kovarianz von 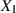 und
und 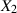 .
.
Die Kovarianz 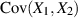 kann auch noch anders ausgedrückt werden (Verschiebungssatz), wenn
man
kann auch noch anders ausgedrückt werden (Verschiebungssatz), wenn
man
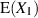 und
und 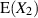 quasi konstante Faktoren sind;
quasi konstante Faktoren sind;
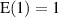 anwendet.
anwendet.
Ist eine der beiden Zufallsgrößen mittelwertfrei, dann entspricht die Kovarianz dem Erwartungswert des Produktes der beiden Größen.
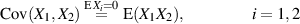 | (25) |
Unter diesen Bedingungen spricht man auch von der Korrelation beider Zufallsgrößen (vgl. Abschnitte 3.4 und 4).
Im Fall 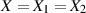 entartet die Kovarianz zur Varianz (siehe Formel 11).
entartet die Kovarianz zur Varianz (siehe Formel 11).
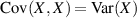
Für kontinuierliche Zufallsgrößen kann die Kovarianz wiefolgt konkretisiert werden:
Dabei geht man davon aus, daß der Vektor 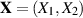 eine zweidimensionale Zufallsgröße mit der
Dichtefunktion
eine zweidimensionale Zufallsgröße mit der
Dichtefunktion 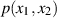 ist. Sind die Zufallsgrößen
ist. Sind die Zufallsgrößen 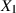 und
und 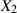 stochastisch unabhängig, dann ist die
Wahrscheinlichkeitsdichte faktorisierbar in
stochastisch unabhängig, dann ist die
Wahrscheinlichkeitsdichte faktorisierbar in
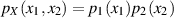
und deshalb auch das Doppelintegral von Gleichung 26.
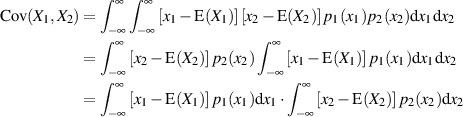
Wegen der allgemeingültigen Beziehung
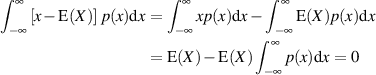
verschwinden aber beide Faktoren, d. h. die Kovarianz (und der Korrelationskoeffizient) unabhängiger Zufallsgrößen ist grundsätzlich Null. Aus Gleichung 24 folgt unter dieser Bedingung ferner:
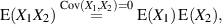 | (27) |
was als Kriterium unkorrelierter Zufallsgrößen in seiner Umkehrung ebenfalls verwendbar ist.
Für einen mehrdimensionalen Zufallsvektor 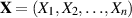 kann man eine sogenannte
Varianz-Kovarianz-Matrix
kann man eine sogenannte
Varianz-Kovarianz-Matrix 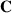 angeben,
angeben,
![ci,k = Cov (Xi,Xk)= E {[Xi− E (Xi)][Xk − E(Xk)]}](probabil208x.png)
deren Elemente 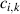 die Kovarianz zwischen der Zufallsgröße
die Kovarianz zwischen der Zufallsgröße 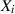 und
und 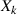 repräsentieren.
repräsentieren.
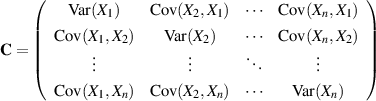
Die Matrix 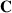 ist
ist
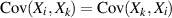 ),
),
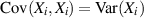 .
.
Der Korrelationskoeffizient ist ein Maß für die Abhängigkeit zweier Zufallsgrößen.11
Zu den Eigenschaften des Korrelationskoeffizienten:
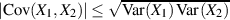 gilt immer:
gilt immer:
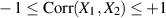 .
.
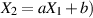 führen immer zu:
führen immer zu: 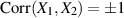 .
.
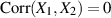 .12
.12 Für mittelwertfreie Zufallsgrößen reduzieren sich Kovarianz und Varianz entsprechend der
Formeln 27 und 13 auf 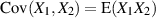 und
und 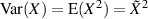 und deshalb der
Korrelationskoeffizient auf
und deshalb der
Korrelationskoeffizient auf
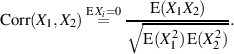 | (29) |