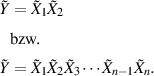Um die Wahrscheinlichkeitsdichte eines Produkts von zwei Zufallsgrößen 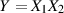 zu bestimmen,
interpretieren wir dieses Produkt wieder als Funktion
zu bestimmen,
interpretieren wir dieses Produkt wieder als Funktion 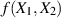 . Da wir auch hier nur eine
Ergebnisgröße, nämlich
. Da wir auch hier nur eine
Ergebnisgröße, nämlich 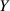 , haben, müssen wir die Darstellung
, haben, müssen wir die Darstellung 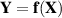 wieder “künstlich”
erzeugen. Dazu benennen wird
wieder “künstlich”
erzeugen. Dazu benennen wird 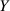 in
in 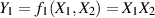 um und definieren eine zweite Funktion
um und definieren eine zweite Funktion
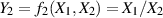 .
.
Auch diesmal ermitteln wir zuerst die Umkehrfunktionen 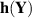 , beschränken uns aber auf die
positiven Werte von
, beschränken uns aber auf die
positiven Werte von 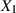 und
und 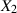 sowie positive Radikanden.
sowie positive Radikanden.
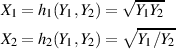
Den Absolutwert der zugehörigen Funktionaldeterminante
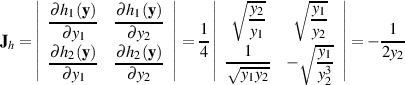
wenden wir wieder auf Gleichung 37 an.
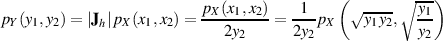
Da die Zufallsgröße 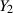 auch hier nicht von Interesse ist, müssen wir sie wieder “ausblenden”, d. h. aus
der verbundenen Dichtefunktion
auch hier nicht von Interesse ist, müssen wir sie wieder “ausblenden”, d. h. aus
der verbundenen Dichtefunktion 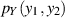 die (eindimensionale) Randdichte von
die (eindimensionale) Randdichte von 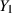 berechnen.
Dabei benennen wir auch gleich wieder
berechnen.
Dabei benennen wir auch gleich wieder 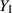 in
in 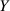 um.
um.

Die abschließende Substitution 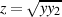 , d. h.
, d. h. 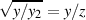 und
und 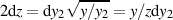 ergibt:
ergibt:
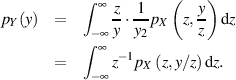
Für die Wahrscheinlichkeitsdichte des Produktes zweier (abhängiger) Zufallsgrößen gilt also:
Sind 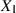 und
und 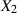 stochastisch unabhängig, d. h. es gilt
stochastisch unabhängig, d. h. es gilt 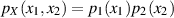 , so vereinfacht sich
Formel 47 zu:
, so vereinfacht sich
Formel 47 zu:
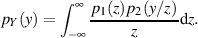 | (48) |
Den Erwartungswert von 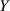 kann man nach der Formel 39 bestimmen. Dazu setzt man als Funktion
kann man nach der Formel 39 bestimmen. Dazu setzt man als Funktion
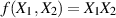 und erhält für den allgemeinen Fall abhängiger Zufallsgrößen:
und erhält für den allgemeinen Fall abhängiger Zufallsgrößen:
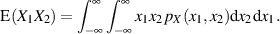 | (49) |
Sind 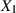 und
und 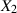 stochastisch unabhängig, d. h. es gibt die Zerlegung
stochastisch unabhängig, d. h. es gibt die Zerlegung 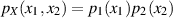 ,
dann kann man weiter vereinfachen
,
dann kann man weiter vereinfachen
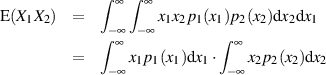
und erhält als Ergebnis:
Verschwindet der Erwartungswert des Produkts sogar überall (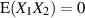 ), dann werden die beiden
Zufallsgrößen als orthogonal zueinander bezeichnet.
), dann werden die beiden
Zufallsgrößen als orthogonal zueinander bezeichnet.
In einer ganz allgemeinen Darstellung führt das Einsetzen von Gleichung 47 in die Formel 10 der Varianz zu:
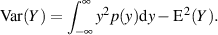
Eine weitere Vereinfachung scheint hier ohne genaue Kenntnis von 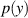 nicht möglich — allerdings
kann man für stochastisch unabhängige Zufallsgrößen mit Hilfe von Formel 48 (und der Substitution
nicht möglich — allerdings
kann man für stochastisch unabhängige Zufallsgrößen mit Hilfe von Formel 48 (und der Substitution
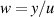 ) noch einen Schritt weiter gehen:
) noch einen Schritt weiter gehen:
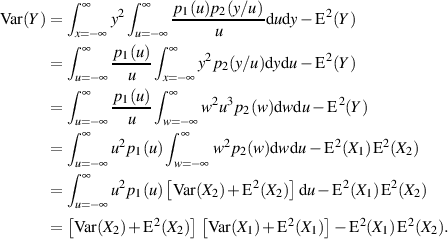
Nimmt man die Definition der Varianz nach Formel 11 hinzu, dann ist die folgende Darstellung gleichwertig:
Für mittelwertfreie Zufallsgrößen (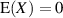 ) geht es dann sogar noch etwas einfacher:
) geht es dann sogar noch etwas einfacher:
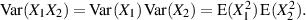
Ausgehend von Gleichung 12 kann der Effektivwert (bei stochastisch unabhängigen Zufallsgrößen) durch Einsetzen der Formeln 50 und 51 leicht ermittelt werden.
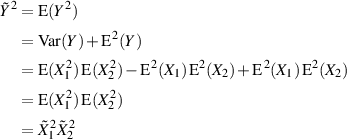
Das Ergebnis ist entsprechend wenig überraschend: