


Ein Vektor 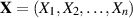 wird
wird  -dimensionale Zufallsgröße genannt,
wenn jede der Einzelgrößen
-dimensionale Zufallsgröße genannt,
wenn jede der Einzelgrößen 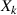 eine Zufallsgröße (über der gleichen
Ereignisalgebra8 )
ist. Die verbundene bzw. gemeinsame Verteilungsfunktion des Zufallsvektors
eine Zufallsgröße (über der gleichen
Ereignisalgebra8 )
ist. Die verbundene bzw. gemeinsame Verteilungsfunktion des Zufallsvektors 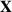
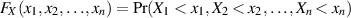
liefert zu jedem Tupel 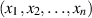 die Wahrscheinlichkeit
die Wahrscheinlichkeit ![Pr[(X1 < x1)∩ (X2 < x2)∩ ⋅⋅⋅∩ (Xn < xn)]](probabil128x.png) .
.
Der Zusammenhang zwischen Dichte- und Verteilungsfunktion hat auch für den Fall einer
mehrdimensionalen Zufallsgröße Bestand, nur daß die Wahrscheinlichkeitsdichte 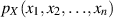 ebenfalls mehrdimensional ist. Für kontinuierliche Zufallsgrößen gibt sie die Wahrscheinlichkeit dafür,
daß
ebenfalls mehrdimensional ist. Für kontinuierliche Zufallsgrößen gibt sie die Wahrscheinlichkeit dafür,
daß 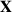 im differentiellen Intervall
im differentiellen Intervall 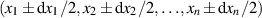 liegt. Integration dieser
infinitesimalen Wahrscheinlichkeiten von
liegt. Integration dieser
infinitesimalen Wahrscheinlichkeiten von  bis
bis  ergibt dann wieder die Verteilungsfunktion von
ergibt dann wieder die Verteilungsfunktion von
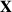 .
.
Umgekehrt läßt sich durch partielle Differentiation nach allen 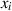 daraus die Dichtefunktion ermitteln.
daraus die Dichtefunktion ermitteln.
Ähnlich zum eindimensionalen Fall lassen sich deshalb die folgenden Eigenschaften von
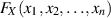 feststellen:
feststellen:
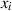 (mit
(mit 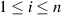 ) gilt:
) gilt: 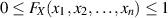 .
.
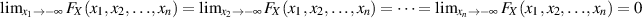 .
.
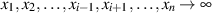 (d. h. alle, außer
(d. h. alle, außer 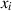 ) entartet
) entartet 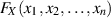 zu
einer eindimensionalen Randverteilung
zu
einer eindimensionalen Randverteilung 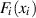 , die nur noch von
, die nur noch von 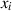 abhängt und die
Wahrscheinlichkeit
abhängt und die
Wahrscheinlichkeit 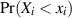 ausdrückt.9
ausdrückt.9
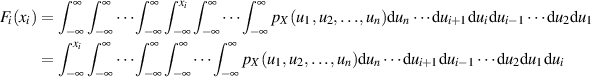
Partielle Differentiation der Randverteilung 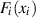 nach
nach 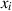 führt zur (Rand-)
Wahrscheinlichkeitsdichte.
führt zur (Rand-)
Wahrscheinlichkeitsdichte.
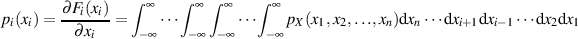
Für den zweidimensionalen Fall (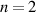 ) lassen sich die Gleichungen folgendermaßen
konkretisieren:
) lassen sich die Gleichungen folgendermaßen
konkretisieren: