


Um die Wahrscheinlichkeitsdichte einer Summe von zwei Zufallsgrößen 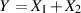 zu bestimmen,
interpretieren wir sie einfach als Funktion
zu bestimmen,
interpretieren wir sie einfach als Funktion 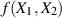 im Sinne des vorigen Abschnitt. Da wir nur eine
Ergebnisgröße, nämlich
im Sinne des vorigen Abschnitt. Da wir nur eine
Ergebnisgröße, nämlich 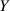 haben, müssen wir die (nach Gleichung 34) notwendige Ordnung
haben, müssen wir die (nach Gleichung 34) notwendige Ordnung 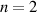 für
für 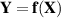 “künstlich” erzeugen. Dazu benennen wird
“künstlich” erzeugen. Dazu benennen wird 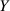 in
in 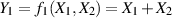 um und
definieren eine zweite Funktion
um und
definieren eine zweite Funktion 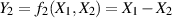 . Bei der Auswahl von
. Bei der Auswahl von 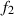 soll nur
Bedingung sein, daß diese Funktion differenzierbar, umkehrbar und nicht linear abhängig von
soll nur
Bedingung sein, daß diese Funktion differenzierbar, umkehrbar und nicht linear abhängig von 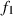 ist.19
ist.19
Zuerst werden die Umkehrfunktionen 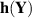 ermittelt
ermittelt
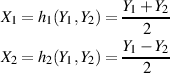
und mit deren Hilfe die Funktionaldeterminante gewonnen.
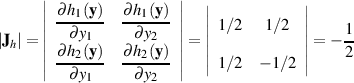
Da in diesem Fall nur lineare Funktionen beteiligt sind, ist die Determinante 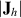 eine Konstante. Wir
reduzieren sie (konform zu Abschnitt 3.2) auf ihren Absolutwert um dann Gleichung 37
anzuwenden.
eine Konstante. Wir
reduzieren sie (konform zu Abschnitt 3.2) auf ihren Absolutwert um dann Gleichung 37
anzuwenden.
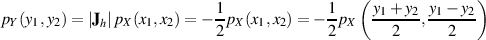
Da die Hilfsgröße 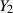 nicht von Interesse ist, müssen wir sie als Zufallsgröße “ausblenden”, d. h. aus
der verbundenen Dichtefunktion
nicht von Interesse ist, müssen wir sie als Zufallsgröße “ausblenden”, d. h. aus
der verbundenen Dichtefunktion 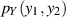 die (eindimensionale) Randdichte von
die (eindimensionale) Randdichte von 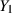 (nach
Formel 20) berechnen. Bei diesem Schritt können wir auch gleich wieder
(nach
Formel 20) berechnen. Bei diesem Schritt können wir auch gleich wieder 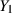 in
in 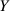 umbenennen, denn
auf diese Größe kam es uns ja an.
umbenennen, denn
auf diese Größe kam es uns ja an.
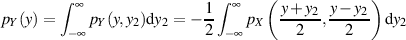
Die abschließende Substitution 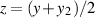 , d. h.
, d. h. 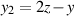 und
und 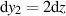 führt zum Ergebnis.
führt zum Ergebnis.
Sind 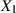 und
und 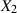 sogar stochastisch unabhängig, d. h. es gilt
sogar stochastisch unabhängig, d. h. es gilt 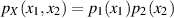 , so
vereinfacht sich Gleichung 40 zu:
, so
vereinfacht sich Gleichung 40 zu:
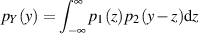 | (41) |
Nach dieser Formel ist die Wahrscheinlichkeitsdichte der Summe zweier unabhängiger Zufallsgrößen also genau die Faltung der einzelnen Dichtefunktionen.20
Für die Summe von  unabhängigen Zufallsgrößen gilt demzufolge:
unabhängigen Zufallsgrößen gilt demzufolge:
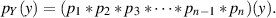
Ausgangspunkt zur Bestimmung des Erwartungswertes der Zufallsgröße 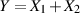 ist dessen
Definitionsgleichung 9.
ist dessen
Definitionsgleichung 9.
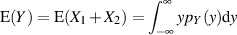
Einsetzen der Wahrscheinlichkeitsdichte von 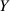 entsprechend Formel 40 ergibt:
entsprechend Formel 40 ergibt:
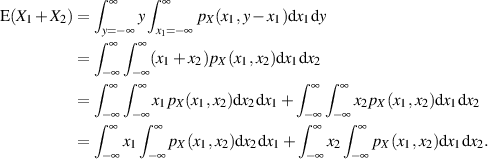
Die inneren Integrale in beiden Summanden stellen nach Gleichung 20 aber genau die Randdichten
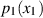 und
und 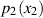 der jeweils anderen Zufallsgröße dar.
der jeweils anderen Zufallsgröße dar.
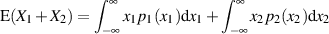
Demzufolge ist der Erwartungswert der Summe zweier Zufallsgrößen unabhängig von der (verbundenen) Wahrscheinlichkeitsdichte einfach die Summe der einzelnen Erwartungswerte [Gne58, § 27].21
Die Varianz der Summe zweier (möglicherweise abhängiger) Zufallsgrößen kann nun ausgehend von Gleichung 11 bestimmt werden.
Mit einem kleinen Rückgriff auf Abschnitt 2.3.3 kann man die letzte Formel auch folgendermaßen schreiben:
Sind die Zufallsgrößen 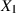 und
und 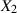 unabhängig, dann gilt
unabhängig, dann gilt 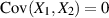 (vgl. Abschnitt 2.3.3)
und deshalb für die Varianz:
(vgl. Abschnitt 2.3.3)
und deshalb für die Varianz:
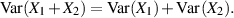
Ausgehend von der Definition des Effektivwertes nach Gleichung 12 kann man hier Zwischenformel 44 des letzten Abschnitts nutzbringend einsetzen.
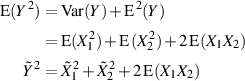
Sind beide Zufallsgrößen sowohl unabhängig als auch (zumindest eine) mittelwertfrei,22 dann berechnet sich der Effektivwert der Summengröße wiefolgt:
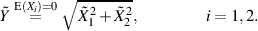
Induktive Fortsetzung ergibt für den Effektivwert der Summe  unabhängiger, mittelwertfreier
Zufallsgrößen in diesem Spezialfall:
unabhängiger, mittelwertfreier
Zufallsgrößen in diesem Spezialfall:
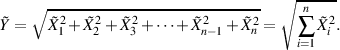
Zwei unabhängige Zufallsgrößen 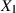 und
und 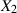 seien normalverteilt
seien normalverteilt
![[ ]
1 1( x− μ )2
pi(x)= √----- exp − -- ----i , i= 1,2
2πσi 2 σi](probabil380x.png) | (46) |
und additiv überlagert.23
Die Berechnung der resultierenden Dichtefunktion 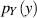 kann dann durch Anwendung
der Faltungsformel 41 erfolgen. Relativ einfach läßt sich eine Faltung mit Hilfe der
FOURIER-Transformation berechnen. Dazu werden die Dichtefunktionen
kann dann durch Anwendung
der Faltungsformel 41 erfolgen. Relativ einfach läßt sich eine Faltung mit Hilfe der
FOURIER-Transformation berechnen. Dazu werden die Dichtefunktionen 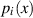 in den Bildbereich
transformiert
in den Bildbereich
transformiert
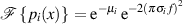
und dann einfach multipliziert (Faltungssatz).
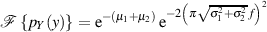
Die Rücktransformation von 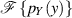 liefert sofort die Lösung.
liefert sofort die Lösung.
![[ ]
1 1 ( x− μ)2 ∘ -------
pY (y) = √-----exp − -- ----- , mit σ = σ21 + σ22, μ = μ1 + μ2
2πσ 2 σ](probabil388x.png)
Die Summe zweier normalverteilter Zufallsgrößen mit den Erwartungswerten 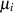 und den
Varianzen
und den
Varianzen 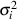 ist wieder normalverteilt mit dem Erwartungswert
ist wieder normalverteilt mit dem Erwartungswert 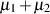 und der Varianz
und der Varianz
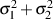 .24
.24