


Die Zufallsgröße 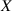 kann in diesem Fall unendlich viele Werte
kann in diesem Fall unendlich viele Werte  aus einem endlichen oder unendlichen Intervall
annehmen.4
Bezieht man sich auf Grenzwerte bzw. infinitesimal große Intervalle, so kann man ausgehend von den
diskreten Zufallsgrößen den Quantifizierungsbegriff der Wahrscheinlichkeit erweitern.
aus einem endlichen oder unendlichen Intervall
annehmen.4
Bezieht man sich auf Grenzwerte bzw. infinitesimal große Intervalle, so kann man ausgehend von den
diskreten Zufallsgrößen den Quantifizierungsbegriff der Wahrscheinlichkeit erweitern.
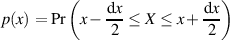
Die (jetzt) kontinuierliche Größe 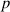 gibt die Wahrscheinlichkeit an, mit der die Zufallsgröße
gibt die Wahrscheinlichkeit an, mit der die Zufallsgröße 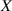 einen Wert
einen Wert  in der Umgebung
in der Umgebung 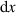 annimmt. Dadurch erhält
annimmt. Dadurch erhält 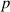 differentiellen Charakter,
weshalb
differentiellen Charakter,
weshalb 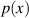 auch als Dichtefunktion bezeichnet wird. Die Wahrscheinlichkeit
auch als Dichtefunktion bezeichnet wird. Die Wahrscheinlichkeit 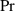 , daß
, daß 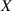 einen Wert innerhalb eines Intervalls
einen Wert innerhalb eines Intervalls ![[a,b]](probabil87x.png) annimmt, muß nun durch Integration bestimmt
werden.
annimmt, muß nun durch Integration bestimmt
werden.
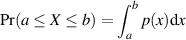 | (4) |
Wie bei den diskreten Zufallsgrößen muß die Wahrscheinlichkeit, daß 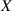 einen Wert im Intervall
einen Wert im Intervall
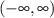 annimmt, Eins sein.
annimmt, Eins sein.
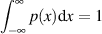 | (5) |
Wegen der Notwendigkeit in Gleichung 4 zu integrieren, wird oft die sogenannte Verteilungsfunktion
einer kontinuierlichen Zufallsgröße 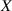 angegeben.
angegeben.
Man kann sich die Verteilungsfunktion nach dieser Formel auch als infinitesimale Addition aller
Einzelwahrscheinlichkeiten 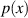 von
von  bis
bis  vorstellen, also in “Summe”
vorstellen, also in “Summe” 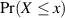 .
. 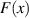 ist
deshalb auch immer eine monoton steigende Funktion mit den Grenzwerten
ist
deshalb auch immer eine monoton steigende Funktion mit den Grenzwerten 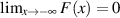 und
und
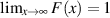 .
.
Nach dem Hauptsatz der Differential- und Integralrechnung gilt für die Wahrscheinlichkeitsdichte im Umkehrschluß:
Die Existenz des uneigentlichen Integrals in Definitionsgleichung 6 vorausgesetzt, kann die
Wahrscheinlichkeit 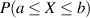 jetzt sehr einfach berechnet werden.
jetzt sehr einfach berechnet werden.
Der Erwartungswert ergibt sich wie bei den diskreten Zufallsgrößen – jetzt wird aber jeder Wert mit der differentiellen Wahrscheinlichkeit seines Auftretens multipliziert.5
In ähnlicher Art und Weise (und unter Berücksichtigung von Formel 5) ergibt sich für die Varianz:6
![∫ ∞
Var(X )= [x− E(X)]2p(x)dx
− ∞](probabil109x.png) | (10) |
und im weiteren
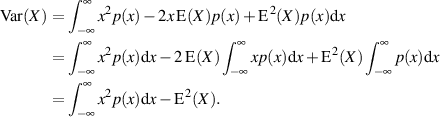
Die Varianz ist also der quadratische Erwartungswert abzüglich des Quadrats des Erwartungswertes der Zufallsgröße.
Umgekehrt gilt:
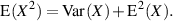 | (12) |
Für Zufallsgrößen mit verschwindendem Mittelwert ist die Varianz gleich dem Quadrat des Effektivwertes.7
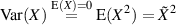 | (13) |
Eine der einfachsten Wahrscheinlichkeitsverteilungen ist die sogenannte Gleichverteilung. Sie hat auf
dem Intervall ![[a,b]](probabil116x.png) eine konstante Wahrscheinlichkeitsdichte
eine konstante Wahrscheinlichkeitsdichte 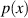 und ist außerhalb dessen Null.
Wegen der Bedingung
und ist außerhalb dessen Null.
Wegen der Bedingung
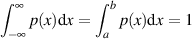
muß sie folgender Gleichung für die Dichtefunktion genügen:
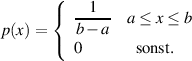 | (14) |
Der Erwartungswert nach Formel 9 bestimmt sich aus den Intervallgrenzen zu
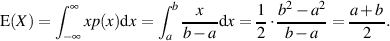 | (15) |
Die Varianz ermittelt sich nach Formel 10 ebenfalls relativ einfach.