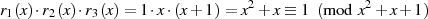Ein Erweiterungskörper  ist ein Körper
ist ein Körper  , der einen anderen Körper
, der einen anderen Körper  als
Teilkörper enthält [PW72, 6.5]. Der Grad der Körpererweiterung von
als
Teilkörper enthält [PW72, 6.5]. Der Grad der Körpererweiterung von 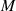 über
über 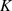 ist die
Dimension von
ist die
Dimension von 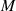 als (so genannter)
als (so genannter)  -Vektorraum und wird als
-Vektorraum und wird als ![[M :K]](algebra720x.png) bzw.
bzw. 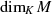 geschrieben. Jeder Vektor in
geschrieben. Jeder Vektor in 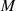 besteht entsprechend der Definition des Vektorraumes (vgl.
Abschnitt 1.4) aus jeweils
besteht entsprechend der Definition des Vektorraumes (vgl.
Abschnitt 1.4) aus jeweils ![[M :K]](algebra723x.png) Tupeln in
Tupeln in  . Bekannte Beispiele für Körpererweiterungen
sind:
. Bekannte Beispiele für Körpererweiterungen
sind:

Ausgehend von den Vorbetrachtungen konstruieren wir jetzt einen endlichen Polynomring ![(K[x],+,⋅)](algebra726x.png) auf dem Körper
auf dem Körper 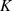 .
.
Darin seien die üblichen Polynomoperationen, wie Addition und Multiplikation gültig, weshalb man
auch von einem Vektorraum der Polynome in der Unbestimmten  mit Koeffizienten aus dem Körper
mit Koeffizienten aus dem Körper
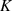 spricht. Ist der Leitkoeffizient
spricht. Ist der Leitkoeffizient  , dann wird das Polynom als normiert (monisch)
bezeichnet, sonst ist
, dann wird das Polynom als normiert (monisch)
bezeichnet, sonst ist 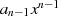 das so genannte Leitmonom.
das so genannte Leitmonom.
Wird anschließend eine Restklassendivision dieser Polynome 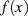 durch ein Polynom
durch ein Polynom 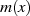 mit Grad
mit Grad  definiert, also
definiert, also 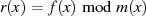 mit
mit ![r(x)∈ K [x]∕m(x)](algebra737x.png) , dann bildet die
Menge der darin enthaltenen Restklassen wieder einen Restklassenring [PW72, 6.], [MvV92,
2.5.4].
, dann bildet die
Menge der darin enthaltenen Restklassen wieder einen Restklassenring [PW72, 6.], [MvV92,
2.5.4].
Der Polynom-Restklassenring auf dem Grundkörper  Im Beispiel des Restklassenringes
Im Beispiel des Restklassenringes ![ℤp [x]∕m(x)](algebra739x.png) lassen sich die Eigenschaften eines Ringes (siehe
Abschnitt 1.2) wiefolgt nachweisen:
lassen sich die Eigenschaften eines Ringes (siehe
Abschnitt 1.2) wiefolgt nachweisen:
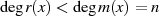 gilt, bildet
gilt, bildet ![K [x]∕m (x)](algebra741x.png) eine additive ABEL’sche Gruppe.
eine additive ABEL’sche Gruppe.
![(K [x]∕m(x),⋅)](algebra750x.png) ist eine multiplikative Halbgruppe, denn:
ist eine multiplikative Halbgruppe, denn:
![(K [x]∕m(x),⋅)](algebra751x.png) abgeschlossen, d. h. wenn
abgeschlossen, d. h. wenn
![r(x),g(x)∈ K [x]∕m(x)](algebra752x.png) angenommen wird, dann gilt für die Multiplikation
angenommen wird, dann gilt für die Multiplikation
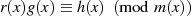 gleichfalls
gleichfalls ![h(x)∈ K[x]∕m (x)](algebra754x.png) .
.
![r(x)[g(x)h(x)]= [r(x)g(x)]h(x)](algebra755x.png) ist in einem Restklassenring von
Polynomen erfüllt.
ist in einem Restklassenring von
Polynomen erfüllt.![r(x)[g(x) +h (x)]= r(x)g(x)+ r(x)h(x)](algebra756x.png) .
.
Der Übergang zu einem Körper wird möglich, wenn 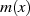 ein Primelement in Bezug auf die Menge der
Polynome
ein Primelement in Bezug auf die Menge der
Polynome ![K [x]](algebra758x.png) ist, es sich also um ein (so genanntes) irreduzibles Polynom handelt. Ein solches Polynom
ist dadurch gekennzeichnet, daß es nicht weiter in Teilpolynome mit Koeffizienten aus
ist, es sich also um ein (so genanntes) irreduzibles Polynom handelt. Ein solches Polynom
ist dadurch gekennzeichnet, daß es nicht weiter in Teilpolynome mit Koeffizienten aus 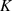 reduzierbar
ist.29
reduzierbar
ist.29
Es sei nun  ein Restklassenpolynom mit Koeffizienten
ein Restklassenpolynom mit Koeffizienten  aus dem endlichen Grundkörper
aus dem endlichen Grundkörper
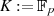 und
und 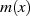 vom Grad
vom Grad  . Dann handelt es sich bei
. Dann handelt es sich bei ![F [x]∕m (x)
p](algebra765x.png) um einen endlichen
Körper mit
um einen endlichen
Körper mit 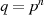 Elementen [Bos96, 3.8]. Man spricht auch von einem Vektorraum
Elementen [Bos96, 3.8]. Man spricht auch von einem Vektorraum 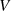 der
Dimension
der
Dimension  über
über  , denn auf diese Weise wird (im Sinne von Abschnitt 1.4) jedem Vektor
, denn auf diese Weise wird (im Sinne von Abschnitt 1.4) jedem Vektor
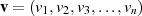 ein Polynom
ein Polynom 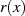 vom Grad
vom Grad 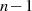 zugeordnet. Es handelt sich folglich nur
um eine andere Darstellung der
zugeordnet. Es handelt sich folglich nur
um eine andere Darstellung der  Tupel des Vektors
Tupel des Vektors  in der Art
in der Art 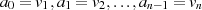 . Die
Potenzen
. Die
Potenzen  bilden die (Polynom-) Basis des Vektorraumes
bilden die (Polynom-) Basis des Vektorraumes 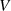 über
über 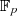 .
Entsprechend ist die Dimension des Erweiterungskörpers
.
Entsprechend ist die Dimension des Erweiterungskörpers 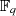 über dem Grundkörper
über dem Grundkörper 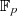 genau
genau
![[Fq :ℤp ]= n](algebra781x.png) . Als Notation für einen solchen Körper wird deshalb auch
. Als Notation für einen solchen Körper wird deshalb auch 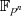 oder
oder  verwendet.
verwendet.
Mit diesen Vorbemerkungen lassen sich alle Aussagen zu Restklassenkörpern, wie sie in Abschnitt 3.3
allgemein formuliert wurden, auf den Erweiterungskörper 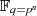 anwenden:
anwenden:
 (Primelement) wird nun als das irreduzible Polynom
(Primelement) wird nun als das irreduzible Polynom 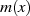 interpretiert.
interpretiert.
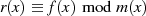 , was grundsätzlich immer
zu einem Grad kleiner als
, was grundsätzlich immer
zu einem Grad kleiner als  für
für 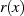 führt.30
Die Kennzeichnung der zu
führt.30
Die Kennzeichnung der zu 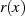 gehörenden Restklasse erfolgt wie gewohnt mit
gehörenden Restklasse erfolgt wie gewohnt mit ![[r(x)]
m(x)](algebra793x.png) ,
wird meistens jedoch weggelassen. Das Element
,
wird meistens jedoch weggelassen. Das Element 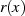 steht also auch hier wieder als
Restklassenvertreter aller Polynome
steht also auch hier wieder als
Restklassenvertreter aller Polynome 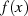 , welche die Bedingung
, welche die Bedingung 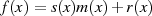 mit
mit 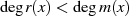 erfüllen.
erfüllen.
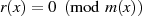 bzw. dessen Restklasse
bzw. dessen Restklasse
![[0]m(x)](algebra799x.png) , das Einselement das Einheitspolynom
, das Einselement das Einheitspolynom 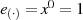 .
.
 sind wohldefiniert und
abgeschlossen, die entsprechenden Gruppen
sind wohldefiniert und
abgeschlossen, die entsprechenden Gruppen 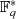 und
und 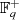 also existent.
also existent.
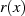 im Restklassenkörper
im Restklassenkörper ![Fp[x]∕m (x)](algebra805x.png) ist aufgrund der Anzahl
von möglichen Koeffizientenkombinationen
ist aufgrund der Anzahl
von möglichen Koeffizientenkombinationen 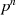 . Bei
. Bei 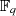 handelt es sich folglich um
einen GALOIS-Körper
handelt es sich folglich um
einen GALOIS-Körper 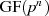 .31
Wegen
.31
Wegen 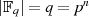 hat dessen multiplikative Gruppe
hat dessen multiplikative Gruppe 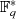 die Ordnung
die Ordnung 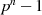 .
.
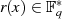 hat eine Ordnung bzw. Periode
hat eine Ordnung bzw. Periode 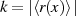 , welche sich aus
Gleichung 2.1 ableitet:
, welche sich aus
Gleichung 2.1 ableitet:
![[r(x)]k − 1 ≡ 0 (mod m (x)).](algebra814x.png)
 des Elements die der multiplikativen
Gruppe
des Elements die der multiplikativen
Gruppe  , d. h.
, d. h. 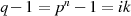 und demzufolge ist
und demzufolge ist
![[r(x)]q−1− 1≡ 0 (mod m(x)).](algebra818x.png) | (3.12) |
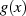 von
von  erfüllt die Bedingung der maximalen Zykluslänge
(Index
erfüllt die Bedingung der maximalen Zykluslänge
(Index 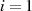 ), hat also die Ordnung
), hat also die Ordnung 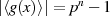 . Es ist damit geeignet, als Basiselement
für die Erzeugung aller anderen Elemente
. Es ist damit geeignet, als Basiselement
für die Erzeugung aller anderen Elemente  verwendet zu werden. Nimmt man das
Nullelement
verwendet zu werden. Nimmt man das
Nullelement 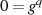 sowie das Einselement
sowie das Einselement 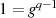 hinzu, so gilt für die Menge der Elemente
hinzu, so gilt für die Menge der Elemente
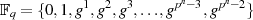 .
.
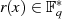 das Modul
das Modul 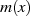 ein Teiler von
ein Teiler von ![q−1
[r(x)] − 1](algebra829x.png) ist, also die Zerlegung
ist, also die Zerlegung
![q−1
[r(x)] − 1 = h(x)m (x)](algebra830x.png) hat. Setzt man insbesondere
hat. Setzt man insbesondere 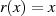 als das kleinste Element (mit
einem Grad größer als
als das kleinste Element (mit
einem Grad größer als 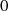 ) aus
) aus 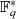 , so erhält man die Beziehungen:
, so erhält man die Beziehungen:
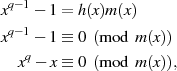
welche auch die Kongruenz 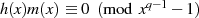 rechtfertigen.
rechtfertigen.
Nach dem Hauptsatz der Zahlentheorie kann man für jede natürliche Zahl eine eindeutigen Primfaktorzerlegung der Form
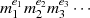
finden. Gleiches trifft auch für Polynome in ![Fp[x]](algebra837x.png) zu, nur daß es sich um irreduzible Polynome anstatt
Primzahlen handelt.
zu, nur daß es sich um irreduzible Polynome anstatt
Primzahlen handelt.
![f(x)= [m1(x)]e1 [m2 (x)]e2[m3 (x)]e3⋅⋅⋅](algebra838x.png)
Jedes der irreduziblen Polynome32
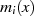 hat eine vom jeweiligen Grad
hat eine vom jeweiligen Grad  abhängige Anzahl von Nullstellen
abhängige Anzahl von Nullstellen 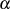 , die entweder im
Grundkörper
, die entweder im
Grundkörper  oder (sämtlich) in einem zugehörigen Erweiterungskörper
oder (sämtlich) in einem zugehörigen Erweiterungskörper 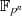 liegen.
Nullstellen im Grundkörper, von denen
liegen.
Nullstellen im Grundkörper, von denen 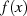 maximal
maximal 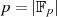 besitzen kann, lassen
sich immer als einfache Faktoren der Art
besitzen kann, lassen
sich immer als einfache Faktoren der Art 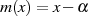 mit
mit 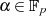 darstellen (vgl.
Beispiel-Faktorisierung von
darstellen (vgl.
Beispiel-Faktorisierung von 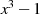 in Abschnitt 3.4.5). Liegen dagegen alle
in Abschnitt 3.4.5). Liegen dagegen alle  Wurzeln von
Wurzeln von 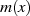 in
einem Erweiterungskörper, dann muß es sich um ein irreduzibles Polynom (höheren Grades)
handeln.33
Ein solcher Körper besteht aus
in
einem Erweiterungskörper, dann muß es sich um ein irreduzibles Polynom (höheren Grades)
handeln.33
Ein solcher Körper besteht aus 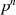 Elementen, welche die
Elementen, welche die 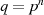 Nullstellen der zugeordneten
Funktion
Nullstellen der zugeordneten
Funktion 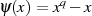 darstellen (vgl. Abschnitt 2.1.5).
darstellen (vgl. Abschnitt 2.1.5). 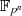 nennt man deshalb auch den kleinsten
Körper über den
nennt man deshalb auch den kleinsten
Körper über den ![ψ (x)∈ Fp[x]](algebra862x.png) vollständig in Linearfaktoren zerfällt [Bos96, 4.5] bzw. kürzer:
vollständig in Linearfaktoren zerfällt [Bos96, 4.5] bzw. kürzer: 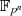 sei der Zerfällungskörper von
sei der Zerfällungskörper von 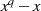 .
.
![ψ(x)= xq− x = ∏ (x − α ), ψ(x)∈ Fp[x]
α∈Fq](algebra865x.png)
Ein weiteres Charakteristikum des Zerfällungskörpers 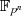 sind die konjugierten Nullstellen, d. h. bei
Kenntnis einer Nullstelle
sind die konjugierten Nullstellen, d. h. bei
Kenntnis einer Nullstelle 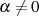 des irreduziblen Polynoms
des irreduziblen Polynoms 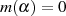 sind die restlichen
sind die restlichen 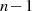 Nullstellen genau die Potenzen
Nullstellen genau die Potenzen 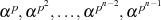 . Das irreduzible Polynom
. Das irreduzible Polynom 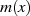 zerfällt also bei Kenntnis nur einer Nullstelle
zerfällt also bei Kenntnis nur einer Nullstelle 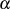 vollständig in seine
vollständig in seine  Linearfaktoren. Der
Beweis dieses Satzes geht vom sogenannten „Anfänger-Traum“ (Freshmans Dream) aus:
Linearfaktoren. Der
Beweis dieses Satzes geht vom sogenannten „Anfänger-Traum“ (Freshmans Dream) aus:
und berücksichtigt dann, daß im Grundkörper  jedes Element
jedes Element  die Relation
die Relation 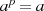 erfüllt (vgl.
Abschnitt 3.3.2).
erfüllt (vgl.
Abschnitt 3.3.2).
![( )
n n n ( ) n p
m (αp)= ∑ aiαip = ∑ api αip = ∑ aiαi p = ∑ aiαi = [m (α)]p = 0
i=0 i=0 i=0 i=0](algebra878x.png)
Aus diesem Grund läßt sich für jedes der irreduziblen Polynome 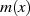 die folgende Linearfaktordarstellung
angeben:34
die folgende Linearfaktordarstellung
angeben:34

Die Nullstellen  kann man (wegen ihrer linearen Unabhängigkeit) verwenden, um statt einer
Polynombasis eine so genannte Normalbasis des Vektorraumes (der Dimension
kann man (wegen ihrer linearen Unabhängigkeit) verwenden, um statt einer
Polynombasis eine so genannte Normalbasis des Vektorraumes (der Dimension  ) über
) über  zu
definieren.
zu
definieren.
 der Faktor
der Faktor  für
für 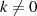 immer durch
immer durch  teilbar ist und folglich
teilbar ist und folglich  gilt.
gilt.
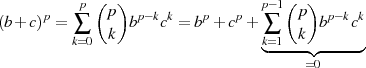
Für eine Erweiterung des Primkörpers  auf
auf  Dimensionen ist ein irreduzibles Polynom
Dimensionen ist ein irreduzibles Polynom 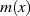 vom Grad
vom Grad  notwendig. Der dadurch entstehende Körper
notwendig. Der dadurch entstehende Körper 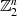 soll am Beispiel des Polynoms
soll am Beispiel des Polynoms
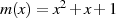 mit Koeffizienten aus
mit Koeffizienten aus 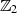 (zu den Rechenoperationen vgl. Seite 58) jetzt
kurz betrachtet werden. Nach Darstellung 3.10 gehören genau
(zu den Rechenoperationen vgl. Seite 58) jetzt
kurz betrachtet werden. Nach Darstellung 3.10 gehören genau  Polynome zum
Erweiterungskörper (
Polynome zum
Erweiterungskörper (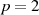 ,
, 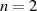 ), nämlich:
), nämlich:

Wie sich leicht feststellen läßt, ist 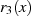 das erzeugende Element der multiplikativen Gruppe
das erzeugende Element der multiplikativen Gruppe
 , denn die anderen Elemente ergeben sich als Potenzen
, denn die anderen Elemente ergeben sich als Potenzen  .
.
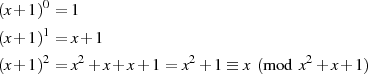
Außerdem sind alle Elemente (abgesehen von  ) wirklich Nullstellen des Polynoms
) wirklich Nullstellen des Polynoms
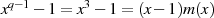 . Auch gut erkennen läßt sich, daß
. Auch gut erkennen läßt sich, daß  für jedes Element
für jedes Element  ein
Teiler von
ein
Teiler von ![[r(x)]q−1− 1](algebra917x.png) ist.
ist.
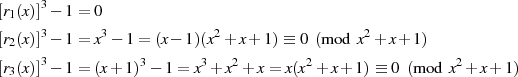
Äquivalent dazu ist das Produkt aller Elemente (konform zu Formel 2.15) genau das neutrale Element 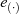 der
multiplikativen Gruppe.35
der
multiplikativen Gruppe.35