


Eine Menge 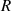 nennt man einen Ring
nennt man einen Ring 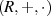 , wenn auf ihr sowohl Addition als auch
Multiplikation mit
, wenn auf ihr sowohl Addition als auch
Multiplikation mit 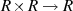 erklärt sind [PW72, 2.2]. Speziell müssen folgende Axiome
gelten:
erklärt sind [PW72, 2.2]. Speziell müssen folgende Axiome
gelten:
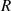 eine ABEL’sche Gruppe
eine ABEL’sche Gruppe 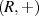 .
.
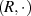 ist eine so genannte Halbgruppe,4
d. h.
ist eine so genannte Halbgruppe,4
d. h.
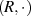 ist abgeschlossen (
ist abgeschlossen (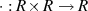 )
)
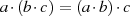 für
für 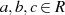 .
.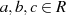 das Distributivgesetz gelten
das Distributivgesetz gelten 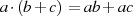 .
.Existiert zusätzlich noch die Identität 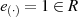 mit
mit 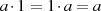 für alle
für alle 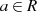 ,
dann wird
,
dann wird 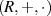 Monoid oder Ring mit Eins genannt. Die Menge der Elemente
Monoid oder Ring mit Eins genannt. Die Menge der Elemente 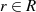 in einem Monoid, welche mit
in einem Monoid, welche mit 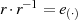 jeweils ein inverses Element besitzen, nennt
man Einheitengruppe
jeweils ein inverses Element besitzen, nennt
man Einheitengruppe 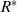 des Ringes. Ein Ring wird außerdem als kommutativ bezeichnet,
wenn auch für die Multiplikation das Kommutativgesetz
des Ringes. Ein Ring wird außerdem als kommutativ bezeichnet,
wenn auch für die Multiplikation das Kommutativgesetz 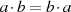 gilt. Ein typisches
Beispiel hierfür ist der Ring
gilt. Ein typisches
Beispiel hierfür ist der Ring 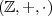 der ganzen Zahlen, denn er erfüllt offensichtlich alle
Axiome.
der ganzen Zahlen, denn er erfüllt offensichtlich alle
Axiome.