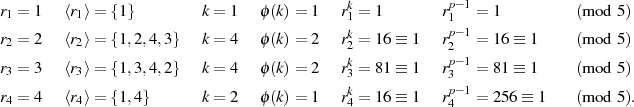Für den Übergang von einem Restklassenring 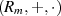 zu einem Restklassenkörper muß man zu
jedem
zu einem Restklassenkörper muß man zu
jedem 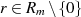 das Vorhandensein eines multiplikativ inversen Elements
das Vorhandensein eines multiplikativ inversen Elements ![−1
[r]m](algebra564x.png) , mit
, mit
![[r]m ⋅[r]m−1 = [1]m](algebra565x.png) , fordern. Wir nehmen die Antwort vorweg und proklamieren, daß es ein solches
Element in
, fordern. Wir nehmen die Antwort vorweg und proklamieren, daß es ein solches
Element in  nur dann gegeben kann, wenn
nur dann gegeben kann, wenn  und
und  teilerfremd sind [PW72, Satz 6.4].
Bezieht man diese Aussage z. B. auf
teilerfremd sind [PW72, Satz 6.4].
Bezieht man diese Aussage z. B. auf  , dann müssen (wenn keine
weiteren Forderungen an
, dann müssen (wenn keine
weiteren Forderungen an  gestellt werden) alle Elemente
gestellt werden) alle Elemente  , für die
, für die 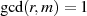 nicht erfüllt
werden kann, ausgeschlossen werden. Sowohl im allgemeinen als auch speziellen Fall von
nicht erfüllt
werden kann, ausgeschlossen werden. Sowohl im allgemeinen als auch speziellen Fall von 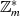 ist
diese Einschränkung grundsätzlich hinfällig, wenn es sich bei
ist
diese Einschränkung grundsätzlich hinfällig, wenn es sich bei  um ein Primelement handelt
(ein vollständiges Restklassensystem) – in Bezug auf
um ein Primelement handelt
(ein vollständiges Restklassensystem) – in Bezug auf  also um eine Primzahl
also um eine Primzahl 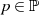 ,
weshalb
,
weshalb 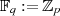 (mit
(mit 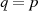 ). Im Fall des Ausschlusses von Elementen (ein reduziertes
Restklassensystem) ist die Anzahl der teilerfremden Zahlen durch EULER’s Totient-Funktion
). Im Fall des Ausschlusses von Elementen (ein reduziertes
Restklassensystem) ist die Anzahl der teilerfremden Zahlen durch EULER’s Totient-Funktion  bestimmt und so die Ordnung der multiplikativen Gruppe
bestimmt und so die Ordnung der multiplikativen Gruppe 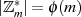 , d. h.
, d. h. 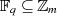 (mit
(mit
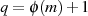 ).
).
Beweis
Ist  kein primes Element, dann läßt es sich mindestens in zwei Faktoren
kein primes Element, dann läßt es sich mindestens in zwei Faktoren 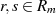 zerlegen (die
nicht Vielfache von
zerlegen (die
nicht Vielfache von  sind, also
sind, also 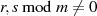 ). Da nun
). Da nun 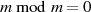 ist, gilt für die
Restklassenmultiplikation
ist, gilt für die
Restklassenmultiplikation ![[r]m ⋅[s]m = [m ]m = 0](algebra588x.png) . Soll aber
. Soll aber ![[r]m](algebra589x.png) eine inverse Restklasse
eine inverse Restklasse ![[r]−m1](algebra590x.png) besitzen, dann kann man beide Seiten des Produktes mit
besitzen, dann kann man beide Seiten des Produktes mit ![[r]m−1](algebra591x.png) multiplizieren.
multiplizieren.
![[r]m−1[r]m ⋅[s]m = [s]m = [r]m−1[m ]m = 0
◟--◝◜--◞
e(⋅)=1](algebra592x.png)
![[s]m](algebra593x.png) ist aber nach Voraussetzung nicht
ist aber nach Voraussetzung nicht 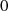 , demzufolge kann ein Inverses zu
, demzufolge kann ein Inverses zu ![[r]m](algebra595x.png) für den Fall dieser
Zerlegung nicht existieren.
für den Fall dieser
Zerlegung nicht existieren.
Im Gegenzug bleibt noch nachzuweisen, daß, wenn  ein Primelement ist, für jede Restklasse
ein Primelement ist, für jede Restklasse ![[r]
m](algebra597x.png) aus
aus 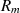 ein inverses Element
ein inverses Element ![−1
[r]m](algebra599x.png) auch wirklich existiert. Zu diesem Zweck betrachten
wir alle
auch wirklich existiert. Zu diesem Zweck betrachten
wir alle ![[r]m ∈ Rm](algebra600x.png) , ausgenommen die Restklasse
, ausgenommen die Restklasse ![[1]m](algebra601x.png) , welche bei der Inversion auf sich
selbst abgebildet wird. Da wegen der Modulo-Reduktion (wir verwenden jetzt wieder den
Vertreter der Restklasse) immer
, welche bei der Inversion auf sich
selbst abgebildet wird. Da wegen der Modulo-Reduktion (wir verwenden jetzt wieder den
Vertreter der Restklasse) immer 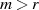 gilt, kann nur
gilt, kann nur  ein Teiler von
ein Teiler von  sein und nicht
umgekehrt. Aber auch dies ist nicht möglich, wenn nach Voraussetzung
sein und nicht
umgekehrt. Aber auch dies ist nicht möglich, wenn nach Voraussetzung  relativ prim zu
relativ prim zu  ist. Deshalb kann der größte gemeinsame Teiler von
ist. Deshalb kann der größte gemeinsame Teiler von  und
und  nur das Einselement sein.
Berücksichtigt man jetzt noch die aus dem euklidischen Algorithmus stammende Erkenntnis
(Satz von BéZOUT, vgl. Abschnitt 4.1), daß der größte gemeinsame Teiler
nur das Einselement sein.
Berücksichtigt man jetzt noch die aus dem euklidischen Algorithmus stammende Erkenntnis
(Satz von BéZOUT, vgl. Abschnitt 4.1), daß der größte gemeinsame Teiler 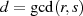 zweier Elemente
zweier Elemente 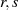 in der Form
in der Form 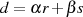 mit
mit 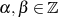 darstellbar ist, dann gilt:
darstellbar ist, dann gilt:
Das inverse Element von ![[r]
m](algebra614x.png) ist demzufolge
ist demzufolge
![[r] −1 = [α] ,
m m](algebra615x.png)
wobei dessen Berechnung z. B. mit Hilfe des erweiterten euklidischen Algorithmus (siehe Abschnitt 4.1.4) möglich ist.19
Da es sich bei den Restklassenkörpern um spezifische GALOIS-Körper handelt, kann man einige
Formeln von Abschnitt 2.2 konkretisieren. Im folgenden sollen deshalb die Körperelemente und deren
Ordnung im Zusammenhang mit der multiplikativen Gruppe  betrachtet werden.
betrachtet werden.
Ordnung von Elementen
Abgesehen von den allgemein geltenden Ordnungsrelationen (siehe Abschnitt 2.1) gibt es speziell für
den Restklassenkörper 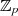 noch eine erwähnenswerte Ausdrucksmöglichkeit für die von einem
Körperelement generierte zyklische Untergruppe:
noch eine erwähnenswerte Ausdrucksmöglichkeit für die von einem
Körperelement generierte zyklische Untergruppe:
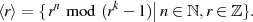 | (3.4) |
Einsichtig wird die Schreibweise sofort, wenn man sie für jeden Exponent  expandiert.20
expandiert.20
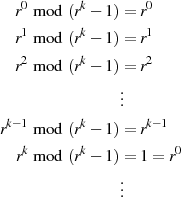
Kleiner Satz von Fermat
Eine für die praktische Anwendung von Restklassenkörpern sehr wichtige Folgerung aus
Gleichung 2.10 ist der (für den Restklassenkörper 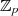 geltende) kleine Satz von FERMAT [PD75, II].
Er resultiert sofort aus
geltende) kleine Satz von FERMAT [PD75, II].
Er resultiert sofort aus 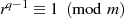 , wenn man berücksichtigt, daß die Ordnung
der multiplikativen Gruppe
, wenn man berücksichtigt, daß die Ordnung
der multiplikativen Gruppe 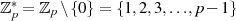 genau
genau  ist.
ist.
Aus dieser Kongruenz kann man wegen 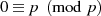 außerdem ableiten, daß
außerdem ableiten, daß 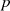 stets ein Teiler von
stets ein Teiler von
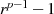 ist.21
ist.21
 | (3.6) |
Obwohl der kleine Satz von FERMAT ursprünglich auf  bezogen war, wird sein Name oft auch in
Verbindung mit Ausgangsformel 2.10 verwendet (siehe zum Beispiel [FHLM04]) — also
ganz allgemein bezogen auf den endlichen Körper
bezogen war, wird sein Name oft auch in
Verbindung mit Ausgangsformel 2.10 verwendet (siehe zum Beispiel [FHLM04]) — also
ganz allgemein bezogen auf den endlichen Körper 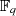 . Deshalb sollen an dieser Stelle
noch weitere Berechnungsmöglichkeiten erwähnt sein, welche sich direkt aus
. Deshalb sollen an dieser Stelle
noch weitere Berechnungsmöglichkeiten erwähnt sein, welche sich direkt aus 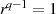 ergeben.
ergeben.
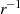 führt z. B. zur Möglichkeit ein Element zu invertieren.
führt z. B. zur Möglichkeit ein Element zu invertieren.
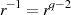
 gibt uns eine weitere Ausdrucksmöglichkeit für das Quadrat eines
Elements.
gibt uns eine weitere Ausdrucksmöglichkeit für das Quadrat eines
Elements.

Satz von Wilson
Betrachtet man die multiplikative Gruppe eines Restklassenkörpers  , so handelt es sich bei den Zahlen
, so handelt es sich bei den Zahlen
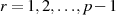 um die
um die 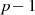 Nullstellen
Nullstellen 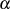 des Polynoms
des Polynoms 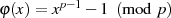 . Anwendung
von Gleichung 2.15 auf
. Anwendung
von Gleichung 2.15 auf 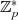 führt folgerichtig zum Satz von WILSON [Sho05, 2.8.1], [PD75, II], [Bun08,
2].23
führt folgerichtig zum Satz von WILSON [Sho05, 2.8.1], [PD75, II], [Bun08,
2].23
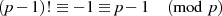 | (3.7) |
Satz von EULER
L. EULER hat für natürliche Zahlen eine sogenannte Totient-Funktion  definiert,
welche die Anzahl der positiven Zahlen (größer als
definiert,
welche die Anzahl der positiven Zahlen (größer als 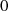 und kleiner als
und kleiner als  ) teilerfremd zu
) teilerfremd zu  ausdrückt.24
Mit Hilfe dieser Funktion hat er FERMAT’s kleinen Satz folgendermaßen verallgemeinert [Sho05, 2.6],
[Bun08, 2], [PD75, II]:
ausdrückt.24
Mit Hilfe dieser Funktion hat er FERMAT’s kleinen Satz folgendermaßen verallgemeinert [Sho05, 2.6],
[Bun08, 2], [PD75, II]:
Sind zwei Zahlen 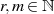 relativ prim zueinander, d. h. sie haben keinen
gemeinsamen Teiler (und so ist
relativ prim zueinander, d. h. sie haben keinen
gemeinsamen Teiler (und so ist  ), dann gilt:
), dann gilt:
Der Beweis ist mit den Betrachtungen von Abschnitt 2.1 zur Ordnung der multiplikativen
Gruppe in 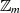 zu erbringen. Danach entspricht die Gruppenordnung
zu erbringen. Danach entspricht die Gruppenordnung 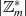 der Anzahl
invertierbarer Elemente (solche mit
der Anzahl
invertierbarer Elemente (solche mit  ), d. h. mit EULER’s Totient-Funktion genau
), d. h. mit EULER’s Totient-Funktion genau
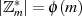 .25
Berücksichtigt man jetzt noch die Gruppen nach Formel 2.10, dann bestätigt sich EULER’s Satz in
Form von Gleichung 2.9.
.25
Berücksichtigt man jetzt noch die Gruppen nach Formel 2.10, dann bestätigt sich EULER’s Satz in
Form von Gleichung 2.9.
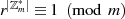
Speziell im Restklassenkörper 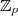 entspringt aus Kongruenz 3.8 mit
entspringt aus Kongruenz 3.8 mit 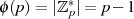 sofort der
kleine Satz von FERMAT.
sofort der
kleine Satz von FERMAT.
Für einen speziellen Fall, nämlich das Produkt zweier Primzahlen 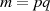 , ist es sehr wünschenswert die Totient-Funktion
zu kennen.26
Sind
, ist es sehr wünschenswert die Totient-Funktion
zu kennen.26
Sind 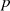 und
und 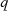 nach Voraussetzung Primzahlen, dann können nur die Zahlen (kleiner als
nach Voraussetzung Primzahlen, dann können nur die Zahlen (kleiner als  )
gemeinsame Teiler mit
)
gemeinsame Teiler mit  haben, die Vielfache von
haben, die Vielfache von  oder
oder 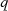 sind. Vielfache von
sind. Vielfache von 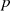 die kleiner als
die kleiner als
 sind, gibt es aber genau
sind, gibt es aber genau 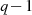 , was für
, was für 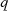 äquivalent gilt (nämlich
äquivalent gilt (nämlich  und
und  ). Somit muß man von den
). Somit muß man von den  Zahlen kleiner als
Zahlen kleiner als  genau
genau
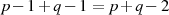 subtrahieren, was zu
subtrahieren, was zu
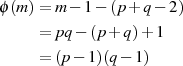
führt.27 In ähnlicher Art und Weise kann man auch die folgende Formel ableiten:
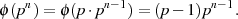
Körper  Der Körper
Der Körper 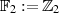 ist von besonderer praktischer Bedeutung, denn er bildet häufig die Grundlage
technischer Realisierungen. Die beiden Elemente von
ist von besonderer praktischer Bedeutung, denn er bildet häufig die Grundlage
technischer Realisierungen. Die beiden Elemente von 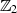 werden mit
werden mit ![{[0]2,[1]2}](algebra695x.png) oder kürzer mit
oder kürzer mit
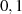 bezeichnet. Wegen ihrer einfachen Implementierung sind die Operationen in
bezeichnet. Wegen ihrer einfachen Implementierung sind die Operationen in 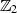 besonders
effizient.
besonders
effizient.
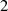 ) ist mit
) ist mitgeradezu primitiv und entspricht dem logischen
Exklusiv-Oder.28
Wie man sofort sieht, ist das neutrale Element die  und wegen Beziehung 3.9 das additiv
Inverse die
und wegen Beziehung 3.9 das additiv
Inverse die 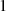 . Addition und Subtraktion sind in diesem Sinne gleichwertig, denn es gilt
. Addition und Subtraktion sind in diesem Sinne gleichwertig, denn es gilt
 .
.

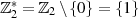 , welches ja
die Bedingung
, welches ja
die Bedingung 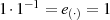 erfüllen muß. Einzig mögliche Schlußfolgerung ist die, daß es
sich bei dem inversen Element
erfüllen muß. Einzig mögliche Schlußfolgerung ist die, daß es
sich bei dem inversen Element 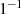 um
um 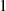 selbst handelt.
selbst handelt.Körper 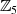 Für den Körper
Für den Körper 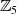 , also dem Fall einer multiplikativen Gruppe der
, also dem Fall einer multiplikativen Gruppe der 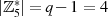 , gilt für die der
Elemente:
, gilt für die der
Elemente: