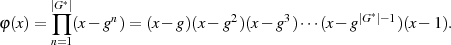Entsprechend Abschnitt 1.1.2 handelt es sich bei endlichen kommutativ-multiplikativen Gruppen um
algebraische Strukturen  , welche bzgl. der Multiplikation
, welche bzgl. der Multiplikation
sind.10
Endliche multiplikative Gruppen sind insbesondere wegen ihrer Eigenschaften beim Potenzieren von
Gruppenelementen sehr interessant. Betrachten wir dazu die Folge der Potenzen 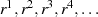 irgendeines Elements
irgendeines Elements  . Nach dem Prinzip der Abgeschlossenheit (Gruppenaxiom)
wird auch jede Potenz von
. Nach dem Prinzip der Abgeschlossenheit (Gruppenaxiom)
wird auch jede Potenz von  wieder in
wieder in 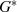 liegen. Wegen der endlichen Zahl
liegen. Wegen der endlichen Zahl  von
Elementen, muß sich ab irgendeiner Potenz
von
Elementen, muß sich ab irgendeiner Potenz 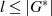 die Folge wiederholen. Eine solche
Wiederholung läßt den Ansatz
die Folge wiederholen. Eine solche
Wiederholung läßt den Ansatz 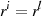 zu. Multiplikation mit dem inversen Element von
zu. Multiplikation mit dem inversen Element von
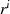 ergibt
ergibt 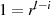 , was wegen
, was wegen 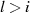 wiederum bedeutet, das es immer ein Element mit
wiederum bedeutet, das es immer ein Element mit
gibt. Die Folge 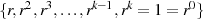 nennt man die vom Element
nennt man die vom Element  erzeugte zyklische
Untergruppe und kennzeichnet sie mit
erzeugte zyklische
Untergruppe und kennzeichnet sie mit
Unter Zuhilfenahme von 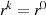 läßt sich die Menge der Elemente auch so definieren:
läßt sich die Menge der Elemente auch so definieren:
Abbildung 2.1 stellt die Periodizität der Folge am Beispiel 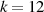 als Kreisteilung dar.
als Kreisteilung dar.
Die Ordnung (Anzahl der Elemente) der Untergruppe 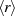 ist
ist 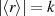 . Sie ist gleichzeitig
die kleinste Potenz
. Sie ist gleichzeitig
die kleinste Potenz 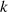 , die zu
, die zu 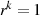 führt. Man nennt sie auch Ordnung des Elements
führt. Man nennt sie auch Ordnung des Elements  und schreibt statt
und schreibt statt 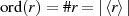 einfach nur
einfach nur 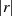 . Die Ordnung des neutralen
Elements
. Die Ordnung des neutralen
Elements 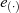 ist
ist 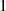 , denn der kleinste Exponent
, denn der kleinste Exponent 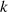 der zu
der zu 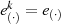 führt, ist
führt, ist
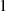 .11
.11
Formel 2.1 gibt uns, wenn man sie mit 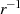 multipliziert, eine Berechnungsvorschrift für das inverse
Element an die Hand:
multipliziert, eine Berechnungsvorschrift für das inverse
Element an die Hand:
Betrachten wir jetzt die  -te Potenz irgendeines Elements
-te Potenz irgendeines Elements  und stellen die Frage nach der Ordnung
des so erzeugten Elements
und stellen die Frage nach der Ordnung
des so erzeugten Elements  .
.
Bezeichnet man dazu mit 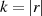 und
und 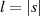 die jeweilige Ordnung, so gilt nach Beziehung 2.1:
die jeweilige Ordnung, so gilt nach Beziehung 2.1:

und für weitere Potenzen von 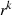 :
:
Unter diesen Voraussetzungen kann man
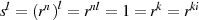
formulieren und so  schlußfolgern (Exponentenvergleich). Da sich unser Interesse auf den
kleinsten Exponenten
schlußfolgern (Exponentenvergleich). Da sich unser Interesse auf den
kleinsten Exponenten  beschränkt, haben wir es hierbei mit der Frage nach dem kleinsten
gemeinsamen Vielfachen von
beschränkt, haben wir es hierbei mit der Frage nach dem kleinsten
gemeinsamen Vielfachen von  und
und 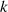 zu tun. Ein Beispiel für
zu tun. Ein Beispiel für  und
und 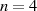 , also
, also
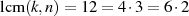 zeigt Abbildung 2.2.
zeigt Abbildung 2.2.
Obwohl mit  auch eine Berechnungsvorschrift
zur Verfügung steht, wollen wir aus Verständnis-gründen den ausführlichen Weg beschreiten. Dazu
wird unter Zuhilfenahme der Abkürzung
auch eine Berechnungsvorschrift
zur Verfügung steht, wollen wir aus Verständnis-gründen den ausführlichen Weg beschreiten. Dazu
wird unter Zuhilfenahme der Abkürzung 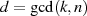 und mittels der Produktdarstellungen
und mittels der Produktdarstellungen 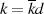 und
und 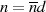 zuerst der gemeinsame Teiler
zuerst der gemeinsame Teiler  eliminiert.
eliminiert.
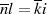 | (2.6) |
Wegen der Teilerfremdheit von 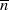 und
und 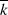 kann nur die Multiplikation mit der jeweils anderen Größe
zum kleinsten gemeinsamen Vielfachen
kann nur die Multiplikation mit der jeweils anderen Größe
zum kleinsten gemeinsamen Vielfachen 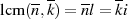 führen.
führen.
Die Konsequenzen aus dem Ergebnis
sind recht interessant:
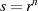 ist immer kleiner/gleich
der Ordnung des Ausgangselements
ist immer kleiner/gleich
der Ordnung des Ausgangselements  . Für den Fall
. Für den Fall 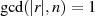 ist sie maximal
(siehe auch Punkt 4).
ist sie maximal
(siehe auch Punkt 4).
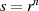 genau die Ordnung von
genau die Ordnung von  teilt.12
Im Sinne der Definition des Index einer Gruppe über deren Untergruppe, hier von
teilt.12
Im Sinne der Definition des Index einer Gruppe über deren Untergruppe, hier von  über
über 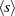 , gilt deshalb:
, gilt deshalb:
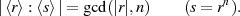
Die Ordnung 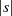 ist dabei (entsprechend der Bedeutung eines größten gemeinsamen
Teilers) der bezüglich
ist dabei (entsprechend der Bedeutung eines größten gemeinsamen
Teilers) der bezüglich  teilerfremde Anteil in
teilerfremde Anteil in 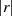 .
.
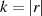 ist automatisch die Ordnung jedes Elements in der
zyklischen Untergruppe
ist automatisch die Ordnung jedes Elements in der
zyklischen Untergruppe 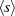 bekannt (vgl. Formel 2.8 mit Mengendefinition 2.2).
bekannt (vgl. Formel 2.8 mit Mengendefinition 2.2).
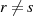 mit derselben Ordnung sind nach Formel 2.8 dadurch gekennzeichnet,
daß
mit derselben Ordnung sind nach Formel 2.8 dadurch gekennzeichnet,
daß 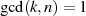 gilt. Die Anzahl der zur Ordnung
gilt. Die Anzahl der zur Ordnung 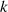 teilerfremden Zahlen (die kleiner
als
teilerfremden Zahlen (die kleiner
als  sind) entspricht damit der Anzahl von möglichen Potenzen
sind) entspricht damit der Anzahl von möglichen Potenzen  , für die
, für die 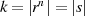 wird. Aus diesem Grund wird in einer multiplikativen Gruppe die Anzahl der Elemente
mit jeweils gleicher Ordnung
wird. Aus diesem Grund wird in einer multiplikativen Gruppe die Anzahl der Elemente
mit jeweils gleicher Ordnung 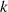 genau durch EULER’s Totient-Funktion13
genau durch EULER’s Totient-Funktion13
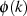 bestimmt.
bestimmt.
 beim Übergang zu dessen Inversen
beim Übergang zu dessen Inversen 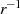 nicht ändert:
nicht ändert:
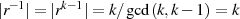 .
.Variante 1
Die Ordnung der von  erzeugten zyklischen Untergruppe
erzeugten zyklischen Untergruppe 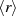 ist nach dem Satz von
LAGRANGE (siehe Abschnitt 1.1.1) ein Teiler der Gruppenordnung
ist nach dem Satz von
LAGRANGE (siehe Abschnitt 1.1.1) ein Teiler der Gruppenordnung 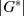 . Man kann die
Ordnung der multiplikativen Gruppe deshalb auch folgendermaßen ausdrücken [Bos96, 1.2,
Satz 3]:
. Man kann die
Ordnung der multiplikativen Gruppe deshalb auch folgendermaßen ausdrücken [Bos96, 1.2,
Satz 3]:
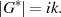 | (2.9) |
Daß die Ordnung von  ein Teiler von
ein Teiler von 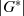 ist, führt in Verbindung mit Gleichung 2.1 zu:
ist, führt in Verbindung mit Gleichung 2.1 zu:
Anschaulich (siehe auch Abbildung 2.2) bedeutet dies, daß sich die Potenzen 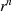 nach
nach  Elementen
periodisch wiederholen
.
Elementen
periodisch wiederholen
.
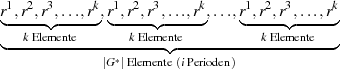
Variante 2
Möchte man einen Rückgriff auf den Satz von LAGRANGE vermeiden, so kann für Beziehung 2.9
auch der folgende Beweis angeführt werden. Multipliziere jedes der  Elemente aus
Elemente aus
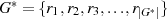 mit dem Element
mit dem Element  , welches ebenfalls
, welches ebenfalls  entstammt (
entstammt ( ist eines der
ist eines der 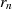 ,
mit
,
mit 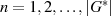 ). Nach dem Prinzip der Abgeschlossenheit muß auch jedes Produkt
). Nach dem Prinzip der Abgeschlossenheit muß auch jedes Produkt 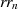 wieder
in
wieder
in 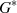 liegen. Außerdem müssen die Produkte paarweise verschieden sein, sonst würde die
Multiplikation mit dem inversen Element
liegen. Außerdem müssen die Produkte paarweise verschieden sein, sonst würde die
Multiplikation mit dem inversen Element 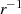 zu zwei gleichen Elementen führen (Bed.
zu zwei gleichen Elementen führen (Bed.  ).
Abgesehen von der Reihenfolge kann deshalb folgende eindeutige Mengenabbildung (Bijektion)
angegeben werden:
).
Abgesehen von der Reihenfolge kann deshalb folgende eindeutige Mengenabbildung (Bijektion)
angegeben werden: 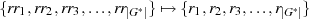 . Bildet man jetzt das Produkt aller
so erzeugten Elemente
. Bildet man jetzt das Produkt aller
so erzeugten Elemente
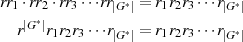
und multipliziert noch mit den Inversen 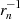 , dann bestätigt sich
, dann bestätigt sich 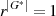 . Einzig mögliche
Schlußfolgerung aus
. Einzig mögliche
Schlußfolgerung aus 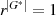 und
und 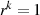 kann aber (konform zu Beziehung 2.9) nur die sein, daß
die Elementeordnung
kann aber (konform zu Beziehung 2.9) nur die sein, daß
die Elementeordnung 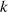 genau die Gruppenordnung
genau die Gruppenordnung 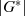 teilt.
teilt.
Allgemein nennt man jede, von mindestens einem Element 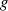 durch Potenzierung erzeugte
multiplikative Gruppe, eine zyklische Gruppe (siehe Abschnitt 2.1.1). Umfaßt die von
durch Potenzierung erzeugte
multiplikative Gruppe, eine zyklische Gruppe (siehe Abschnitt 2.1.1). Umfaßt die von 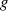 erzeugte
Untergruppe
erzeugte
Untergruppe 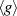 alle Elemente der multiplikativen Gruppe
alle Elemente der multiplikativen Gruppe  (in irgendeiner Abfolge), dann
bezeichnet man
(in irgendeiner Abfolge), dann
bezeichnet man 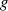 als Generatorelement oder primitives Element.
als Generatorelement oder primitives Element.
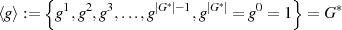 | (2.11) |
Die Ordnung eines solchen Elements muß in diesem Sinne der Gruppenordnung entsprechen.14
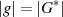
Wie alle anderen Elemente muß auch ein Generatorelement Gleichung 2.1 erfüllen - aber eben nur für
Generatorelemente ist 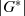 der kleinste Exponent, welcher zu
der kleinste Exponent, welcher zu 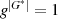 führt. Bei Kenntnis eines
Generatorelements aus
führt. Bei Kenntnis eines
Generatorelements aus 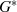 sind so nicht nur alle Elemente der multiplikativen Gruppe bekannt,
sondern nach Formel 2.8 auch deren Ordnung.
sind so nicht nur alle Elemente der multiplikativen Gruppe bekannt,
sondern nach Formel 2.8 auch deren Ordnung.
Um die Frage zu beantworten, ob es immer mindestens ein Generatorelement gibt, rekapitulieren wir folgende Fakten:
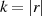 eines jeden Elements teilt die Gruppenordnung (Formel 2.9):
eines jeden Elements teilt die Gruppenordnung (Formel 2.9):
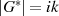 .
.
 kann durch Potenzieren aus
kann durch Potenzieren aus 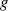 erzeugt werden:
erzeugt werden:  .
.
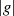 eines Generatorelements erfüllt (wie die eines jeden anderen Elements)
Formel 2.8:
eines Generatorelements erfüllt (wie die eines jeden anderen Elements)
Formel 2.8: 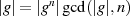 .
.
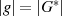 .
.Kombination der formelmäßigen Voraussetzungen ergibt:
und diese Bedingung muß für irgendeine Potenz  zu gewährleisten sein (und zwar
eindeutig für jedes Element
zu gewährleisten sein (und zwar
eindeutig für jedes Element  ). Äquivalenz 2.12 kann aber nur erfüllt werden, wenn man
). Äquivalenz 2.12 kann aber nur erfüllt werden, wenn man  , mit
, mit
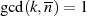 annimmt. Die Anzahl der teilerfremden Zahlen
annimmt. Die Anzahl der teilerfremden Zahlen  kleiner als
kleiner als 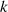 liefert mit
liefert mit 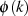 EULER’s
Totient-Funktion (vgl. Abschnitt 3.3.2). Sie ist immer größer als
EULER’s
Totient-Funktion (vgl. Abschnitt 3.3.2). Sie ist immer größer als 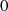 , weshalb stets ein primitives
Element existiert. Aus diesem Grund ist jede multiplikative ABEL’sche Gruppe zyklisch, mit
, weshalb stets ein primitives
Element existiert. Aus diesem Grund ist jede multiplikative ABEL’sche Gruppe zyklisch, mit 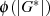 Generatorelementen.15
Generatorelementen.15
Wenden wir uns jetzt einer etwas anderen Sichtweise auf die Elemente der multiplikativen
Gruppe 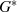 zu, nämlich der Betrachtung über Nullstellen. Dazu gehen wir von dem Polynom
zu, nämlich der Betrachtung über Nullstellen. Dazu gehen wir von dem Polynom
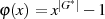 mit
mit  aus, welches die Nullstellen bzw. Einheitswurzeln
aus, welches die Nullstellen bzw. Einheitswurzeln 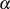 haben
soll.
haben
soll.
Wir stellen nun fest, daß entsprechend des Fundamentalsatzes der Algebra 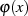 genau
genau 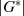 Nullstellen haben muß. Nach Formel 2.9 wird diese Bedingung aber auch durch jedes Element aus
Nullstellen haben muß. Nach Formel 2.9 wird diese Bedingung aber auch durch jedes Element aus 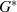 erfüllt. Da deren Anzahl genau mit der Anzahl der Nullstellen übereinstimmt, kann es sich bei den
Elementen
erfüllt. Da deren Anzahl genau mit der Anzahl der Nullstellen übereinstimmt, kann es sich bei den
Elementen 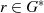 nur um die
nur um die 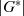 Nullstellen von
Nullstellen von  handeln [PW72, Satz 6.18]. Das
mehrfache Nullstellen nicht vorhanden sind, kann man (in Verbindung mit Gleichung 2.13) durch
Ableitung von
handeln [PW72, Satz 6.18]. Das
mehrfache Nullstellen nicht vorhanden sind, kann man (in Verbindung mit Gleichung 2.13) durch
Ableitung von  an den Stellen
an den Stellen 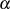 nachprüfen.
nachprüfen.
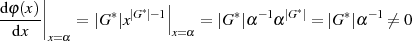
Mit diesen Erkenntnissen läßt sich für 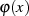 eine Linearfaktordarstellung auf Basis der Elemente
eine Linearfaktordarstellung auf Basis der Elemente  angeben.
angeben.
Ausmultiplizieren der rechten Seite führt mit 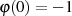 noch zu der interessanten Äquivalenz:
noch zu der interessanten Äquivalenz:
Da alle Elemente  der multiplikativen Gruppe
der multiplikativen Gruppe 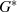 als Potenzen eines Generatorelements
als Potenzen eines Generatorelements 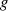 darstellbar sind, kann man die Linearfaktordarstellung 2.14 auch folgendermaßen schreiben:
darstellbar sind, kann man die Linearfaktordarstellung 2.14 auch folgendermaßen schreiben: