


Eine Menge von Vektoren 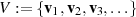 , jeder bestehend aus einem geordneten
, jeder bestehend aus einem geordneten  -Tupel von
Elementen
-Tupel von
Elementen  aus einem Körper
aus einem Körper 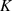 , wird Vektorraum über dem Körper
, wird Vektorraum über dem Körper 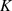 genannt (vgl. [PW72,
2.5]), wenn:
genannt (vgl. [PW72,
2.5]), wenn:
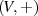 existiert und vom ABEL’schen Typ ist (
existiert und vom ABEL’schen Typ ist (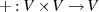 );7
);7
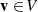 die Multiplikation mit einem Körperelement (Skalar)
die Multiplikation mit einem Körperelement (Skalar)  definiert
ist und wieder zu einem Vektor
definiert
ist und wieder zu einem Vektor 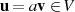 führt (Abgeschlossenheit der Abbildung
führt (Abgeschlossenheit der Abbildung
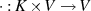 );8
);8
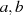 und der Vektoren
und der Vektoren  die folgenden Distributivgesetze
gelten:
die folgenden Distributivgesetze
gelten: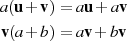
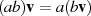 gilt;
gilt;
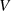 gibt.
gibt.Wenn mit  die Anzahl der Tupel eines Vektors
die Anzahl der Tupel eines Vektors  bezeichnet wird, dann nennt man den zugehörigen
Vektorraum (über dem Körper
bezeichnet wird, dann nennt man den zugehörigen
Vektorraum (über dem Körper 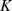 ) üblicherweise
) üblicherweise 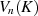 oder kurz
oder kurz 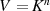 , also z. B.
, also z. B. 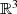 oder
oder 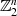 .
Entsprechend ist auch das neutrale Element, welches als
.
Entsprechend ist auch das neutrale Element, welches als 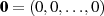 geschrieben wird, ein Vektor
mit
geschrieben wird, ein Vektor
mit  Elementen.
Elementen.
Kann man jeden Vektor von 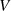 als Linearkombination von unabhängigen Vektoren
als Linearkombination von unabhängigen Vektoren
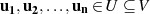 darstellen, also als
darstellen, also als
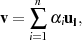
so nennt man 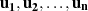 die Basis,
die Basis, 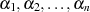 die Koeffizienten und
die Koeffizienten und 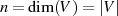 die
Dimension von
die
Dimension von 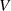 .
.