


Der Algorithmus von EUKLID berechnet den größten gemeinsamen Teiler 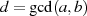 zweier
natürlicher Zahlen
zweier
natürlicher Zahlen 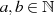 . Die grundlegende, iterativ angewendete Rechenoperation dabei ist modulare
Division.36
Algorithmus 1 beschreibt das klassische Verfahren [Knu98, Sho05, CP05, MvV92, Ber84].
Es beginnt unter der Voraussetzung
. Die grundlegende, iterativ angewendete Rechenoperation dabei ist modulare
Division.36
Algorithmus 1 beschreibt das klassische Verfahren [Knu98, Sho05, CP05, MvV92, Ber84].
Es beginnt unter der Voraussetzung 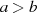 mit einer Modulo-Division
mit einer Modulo-Division 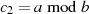 . Im
nächsten Schritt wird
. Im
nächsten Schritt wird  als Modul verwendet und
als Modul verwendet und  berechnet, wonach
berechnet, wonach
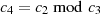 folgt usw. . Diese (wegen
folgt usw. . Diese (wegen 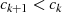 ) absteigende Sequenz endet wenn
) absteigende Sequenz endet wenn  wird37
– das Ergebnis
wird37
– das Ergebnis 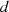 befindet sich dann in
befindet sich dann in 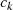 .
.
Beweis
Jeder Iterationsschritt 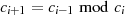 kann in der Umkehrung (vgl. Restklassenbeziehung 3.2 in
Abschnitt 3) als
kann in der Umkehrung (vgl. Restklassenbeziehung 3.2 in
Abschnitt 3) als
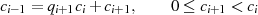
geschrieben werden. So gesehen wird durch den Algorithmus der folgende Abstieg vorgenommen:

bis  verschwindet.
verschwindet.
Warum 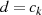 ein gemeinsamer Faktor von
ein gemeinsamer Faktor von  und
und 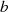 ist, wird klar wenn man die Folge rückwärts
betrachtet. In der letzten Zeile steht
ist, wird klar wenn man die Folge rückwärts
betrachtet. In der letzten Zeile steht 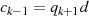 , also teilt
, also teilt  den Rest
den Rest  (oder kürzer
(oder kürzer 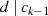 ).
Wenn
).
Wenn 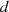 aber als Faktor in
aber als Faktor in 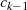 enthalten ist, dann kann man
enthalten ist, dann kann man 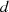 auf der rechten Seite der vorletzten
Gleichung ausklammern, weshalb es auch als Faktor in
auf der rechten Seite der vorletzten
Gleichung ausklammern, weshalb es auch als Faktor in 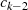 vorkommen muß. Dies setzt sich bis in
die erste Gleichung fort (sämtliche Divisionsreste
vorkommen muß. Dies setzt sich bis in
die erste Gleichung fort (sämtliche Divisionsreste 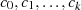 enthalten folglich
enthalten folglich 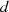 als Teiler), in der
die Startbedingung
als Teiler), in der
die Startbedingung 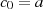 und
und 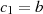 verankert ist. Deshalb ist der gemeinsame Teiler
verankert ist. Deshalb ist der gemeinsame Teiler 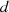 sowohl in
sowohl in
 als auch
als auch 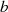 enthalten.
enthalten.
Viel kürzer kann man damit argumentieren, daß die Modulo-Division 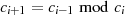 eine GCD erhaltende Operation ist. Denn mit der Zerlegung
eine GCD erhaltende Operation ist. Denn mit der Zerlegung 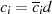 gilt ausgehend von
Formel 3.2:
gilt ausgehend von
Formel 3.2:
d. h. der gemeinsame Teiler  in
in 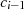 und
und 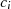 ist auch in
ist auch in 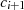 wieder
enthalten.38
wieder
enthalten.38
Damit 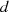 wirklich den größten gemeinsamen Teiler stellt, muß es überhaupt alle gemeinsamen Teiler
enthalten. Mit dem Ziel dies nachzuweisen betrachten wir nochmals die Folge beginnend mit der
vorletzten Gleichung, welche nach
wirklich den größten gemeinsamen Teiler stellt, muß es überhaupt alle gemeinsamen Teiler
enthalten. Mit dem Ziel dies nachzuweisen betrachten wir nochmals die Folge beginnend mit der
vorletzten Gleichung, welche nach 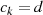 umgestellt wird. Ersetzt man darin
umgestellt wird. Ersetzt man darin 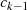 mit Hilfe der
vorvorletzten Gleichung und fährt aufsteigend fort, so erhält man eine lineare Darstellung für
mit Hilfe der
vorvorletzten Gleichung und fährt aufsteigend fort, so erhält man eine lineare Darstellung für
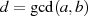 ,
,
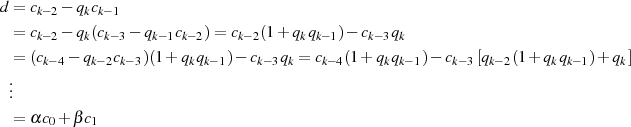
welche auf ganzen Zahlen 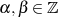 sowie
sowie  und
und 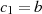 beruht.
beruht.
Mit Hilfe von Formel 4.3, welche auch Satz von BéZOUT genannt
wird,39
kann jetzt relativ einfach bewiesen werden, daß 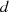 wirklich der größte gemeinsame Teiler ist. Nehmen
wir dazu an, es gäbe einen weiteren gemeinsamen Teiler
wirklich der größte gemeinsame Teiler ist. Nehmen
wir dazu an, es gäbe einen weiteren gemeinsamen Teiler 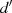 . Dann würde dieser (auf der rechten
Seite von Gleichung 4.3) als Faktor von
. Dann würde dieser (auf der rechten
Seite von Gleichung 4.3) als Faktor von  und
und 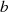 auszuklammern sein und deshalb (wenn
man die linke Seite betrachtet) als Teiler von
auszuklammern sein und deshalb (wenn
man die linke Seite betrachtet) als Teiler von  auftreten. Mit anderen Worten stecken
alle weiteren Teiler (schon) in
auftreten. Mit anderen Worten stecken
alle weiteren Teiler (schon) in  , weshalb nur dieser der größte gemeinsame Teiler sein
kann.
, weshalb nur dieser der größte gemeinsame Teiler sein
kann.
Hinweis
Es existieren unendlich viele lineare Darstellungen für 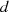 als Linearkombination von
als Linearkombination von  und
und 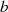 (vgl.
auch die kurze Betrachtung zu diophantischen Gleichungen auf Seite 117). Jede Substitution der Art
(vgl.
auch die kurze Betrachtung zu diophantischen Gleichungen auf Seite 117). Jede Substitution der Art
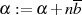 und
und 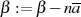 , mit
, mit
erfüllt BéZOUT’s Identität 4.3 ebenso.

Die kleinsten Werte für 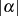 und
und  zeichnen sich folglich durch die Relationen
zeichnen sich folglich durch die Relationen 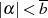 und
und 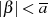 aus. Um sie zu ermitteln kann man entweder
aus. Um sie zu ermitteln kann man entweder 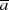 und
und 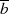 sukzessive von
sukzessive von  und
und  subtrahieren/addieren
oder man reduziert die BéZOUT-Kofaktoren mit Hilfe von
subtrahieren/addieren
oder man reduziert die BéZOUT-Kofaktoren mit Hilfe von 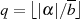 bzw.
bzw. 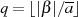 und folgender
Formeln:40
und folgender
Formeln:40

Der erweiterte euklidische Algorithmus erlaubt eine effiziente Berechnung der BéZOUT-Kofaktoren
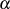 und
und 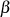 zusammen (und gleichzeitig) mit dem größten gemeinsamen Teiler (siehe
auch [Knu98, Sho05, CP05, Ber84]). Dazu berücksichtigt er einige Erkenntnisse aus dem vorigen
Abschnitt, insbesondere daß:
zusammen (und gleichzeitig) mit dem größten gemeinsamen Teiler (siehe
auch [Knu98, Sho05, CP05, Ber84]). Dazu berücksichtigt er einige Erkenntnisse aus dem vorigen
Abschnitt, insbesondere daß:
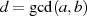 für
für 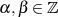 als Linearkombination
als Linearkombination
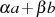 darstellbar ist;
darstellbar ist;
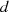 für
für 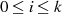 jeden Rest
jeden Rest 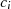 teilt und damit die Darstellung
teilt und damit die Darstellung  rechtfertigt;
rechtfertigt;
 mit Hilfe von
mit Hilfe von 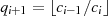 und
und 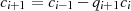 erfolgen kann.
erfolgen kann.Durch Induktion ergibt sich aus
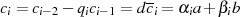 | (4.5) |
wenn man 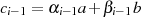 und
und 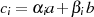 berücksichtigt:
berücksichtigt:
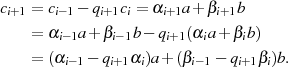
Vergleich mit Ausgangsformel 4.5 erlaubt die Bestimmung von  und
und 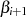 .
.

Mit den Startwerten 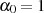 und
und 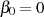 (gewährleistet
(gewährleistet 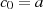 ) bzw.
) bzw. 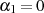 und
und 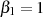 (ebenso
für
(ebenso
für 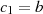 ) kann man den erweiterten euklidischen Algorithmus 2 formulieren.
) kann man den erweiterten euklidischen Algorithmus 2 formulieren.
Er endet ganz genauso wie Algorithmus 1 bei  , ermittelt aber zusätzlich die BéZOUT-Kofaktoren
, ermittelt aber zusätzlich die BéZOUT-Kofaktoren
 und
und 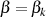 sowie die teilerfremden Anteile
sowie die teilerfremden Anteile 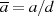 und
und 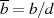 . Letztere findet man
wegen
. Letztere findet man
wegen 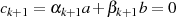 am Ende in
am Ende in 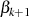 und
und  . Dies wird relativ schnell
aus
. Dies wird relativ schnell
aus
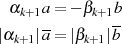
ersichtlich, wenn man auf beiden Seiten der letzten Gleichung das kleinste gemeinsame Vielfache anvisiert.

Hinweis
Als Ergänzung zum Hinweis von Seite 77 kann man sogar feststellen, daß die „Wahl“ von  nicht
unbedingt mit einer Modulo-Division verbunden sein muß. Etwas anders könnte man
nicht
unbedingt mit einer Modulo-Division verbunden sein muß. Etwas anders könnte man 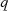 einfach so
wählen, daß
einfach so
wählen, daß
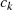 weiterhin eine absteigende Sequenz ist;
weiterhin eine absteigende Sequenz ist;
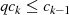 gilt (wodurch
gilt (wodurch  gewährleistet ist).
gewährleistet ist).Den steilsten Abstieg 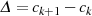 erreicht man allerdings, wenn
erreicht man allerdings, wenn  im jeweiligen
Iterationsschritt maximal ist. Dies ist aber unter der Voraussetzung
im jeweiligen
Iterationsschritt maximal ist. Dies ist aber unter der Voraussetzung 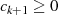 genau bei einer
Modulo-Division
genau bei einer
Modulo-Division 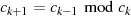 der Fall. Ansonsten ist jeder Wert
der Fall. Ansonsten ist jeder Wert 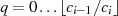 geeignet — einzig die Konvergenzgeschwindigkeit nimmt mit kleineren Werten von
geeignet — einzig die Konvergenzgeschwindigkeit nimmt mit kleineren Werten von 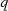 ab.41
ab.41
Für Polynome mit Koeffizienten aus 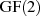 kann man ganz ähnlich verfahren [HMV04,
2.3.6],[Sho05, 17.3], [CP05, 2.2.1], [Ber84, 2.1]. Mit Rückblick auf den Hinweis von Seite 83 muß
man nur folgendes beachten:
kann man ganz ähnlich verfahren [HMV04,
2.3.6],[Sho05, 17.3], [CP05, 2.2.1], [Ber84, 2.1]. Mit Rückblick auf den Hinweis von Seite 83 muß
man nur folgendes beachten:
 ).
).
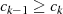 tritt ein Vergleich des
Polynomgrades
tritt ein Vergleich des
Polynomgrades 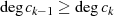 .
.
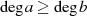 kann entfallen, da der Algorithmus selbst die
Vertauschung der Argumente vornimmt.
kann entfallen, da der Algorithmus selbst die
Vertauschung der Argumente vornimmt.
 läßt sich in folgende Einzelfälle zerlegen:
läßt sich in folgende Einzelfälle zerlegen:
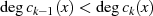 führt zu
führt zu 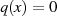 , was nach Algorithmus 3 einer
Vertauschung
, was nach Algorithmus 3 einer
Vertauschung 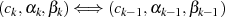 entspricht.
entspricht.
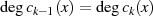 ergibt
ergibt 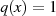 , was mit
, was mit 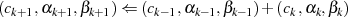 im
nachfolgenden Fall aufgeht.
im
nachfolgenden Fall aufgeht.
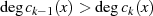 müßte man
müßte man 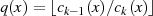 berechnen. Mit
der Option auch ein kleineres
berechnen. Mit
der Option auch ein kleineres 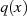 zu verwenden (siehe Hinweis auf Seite 83),
kann man sich eine vollständige Polynomdivision sparen. Stattdessen ist eine
sinnvolle Vorgehensweise sich bei der Divison auf das höchstwertige Bit von
zu verwenden (siehe Hinweis auf Seite 83),
kann man sich eine vollständige Polynomdivision sparen. Stattdessen ist eine
sinnvolle Vorgehensweise sich bei der Divison auf das höchstwertige Bit von
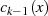 und
und 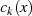 beschränken. In einer monischen Polynomrepräsentation (der
höchstwertige Koeffizient ist 1) führt die Division so zu:
beschränken. In einer monischen Polynomrepräsentation (der
höchstwertige Koeffizient ist 1) führt die Division so zu: 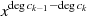 .
.![ℤ2[x]](algebra1096x.png)
Der binäre GCD-Algorithmus kommt im Gegensatz zum klassischen euklidischen Algorithmus ohne
Divisionen aus [CP05, Knu98, Ste67, Wel01]. Statt dessen wird (beginnend mit 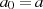 und
und 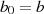 ) durch Subtraktion und Halbierung eine stetige Reduktion der Argumente
) durch Subtraktion und Halbierung eine stetige Reduktion der Argumente  und
und 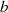 vorgenommen, welche letztlich zum größten gemeinsamen Teiler
vorgenommen, welche letztlich zum größten gemeinsamen Teiler 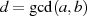 führt.42
führt.42
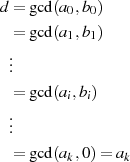
Der Algorithmus endet spätestens dann, wenn im Schritt 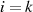 eines der beiden Argumente
eines der beiden Argumente 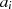 oder
oder
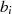 verschwindet (im obigen Fall beispielhaft für
verschwindet (im obigen Fall beispielhaft für 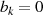 ). Das Reduktionsschema zeigt
Tabelle 4.1.
). Das Reduktionsschema zeigt
Tabelle 4.1.
 |  | 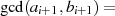 | Begründung |
| gerade |  | gemeinsamer Teiler ist 2 |
|
| gerade | ungerade |  | 2 ist kein gemeinsamer Teiler |
| ungerade | gerade | 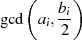 | 2 ist kein gemeinsamer Teiler |
| ungerade,  | 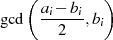 |
|
|
| ungerade,  | 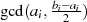 | siehe
Fall
|
|
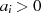 |  |  |
|
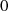 |  |  |
|
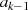 gibt es genau eine Situation, die das Verschwinden von
gibt es genau eine Situation, die das Verschwinden von 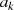 hervorruft
(genauso bezüglich
hervorruft
(genauso bezüglich 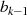 und
und 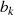 ) . Betrachtet man dazu Tabelle 4.1, so wird
) . Betrachtet man dazu Tabelle 4.1, so wird 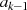 in
folgenden Fällen reduziert:
in
folgenden Fällen reduziert:
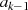 und
und  sind gerade: Halbierung von
sind gerade: Halbierung von 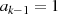 ergibt
ergibt  , bedeutet aber
ungerades
, bedeutet aber
ungerades 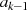 (Widerspruch).
(Widerspruch).
 gerade,
gerade, 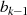 ungerade: Halbierung von
ungerade: Halbierung von 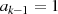 ergibt
ergibt  , was ebenfalls
ungerades
, was ebenfalls
ungerades 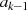 bedeutet (Widerspruch).
bedeutet (Widerspruch).
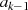 und
und 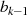 sind ungerade: Halbierung von
sind ungerade: Halbierung von 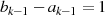 ergibt
ergibt 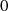 , aber
unter der Voraussetzung
, aber
unter der Voraussetzung 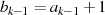 können niemals beide ungerade sein
(Widerspruch).
können niemals beide ungerade sein
(Widerspruch).
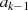 und
und  sind ungerade: Halbierung von
sind ungerade: Halbierung von 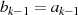 führt zu
führt zu 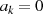 und
stellt damit den einzig möglichen Fall im Schritt
und
stellt damit den einzig möglichen Fall im Schritt 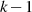 dar.
dar.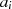 oder
oder 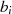 um mindestens ein Bit
reduziert.43
Aus diesem Umstand läßt sich (im Fall
um mindestens ein Bit
reduziert.43
Aus diesem Umstand läßt sich (im Fall 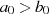 ) für die Anzahl der Iterationsschritte
) für die Anzahl der Iterationsschritte
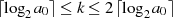 schlußfolgern (vgl. auch [Kal95, Theorem 2]).
schlußfolgern (vgl. auch [Kal95, Theorem 2]).
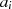 und
und 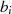 ungerade sind, muß man nicht
unbedingt im Iterationsschritt
ungerade sind, muß man nicht
unbedingt im Iterationsschritt 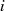 ausführen. Es ist durchaus legitim, falls beispielsweise
ausführen. Es ist durchaus legitim, falls beispielsweise 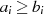 gilt, einfach nur
gilt, einfach nur 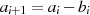 zu berechnen. Die Differenz ergibt ja bekanntlich wieder eine
gerade Zahl (dann ist
zu berechnen. Die Differenz ergibt ja bekanntlich wieder eine
gerade Zahl (dann ist 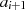 gerade,
gerade, 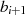 ungerade) und es kommt im nächsten Iterationsschritt
zu der gewünschten Halbierung.
ungerade) und es kommt im nächsten Iterationsschritt
zu der gewünschten Halbierung.
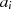 als auch
als auch  gerade sind, kann man grundsätzlich aus der
Haupt-Iterationsschleife herausziehen. Denn wird einmal eines der beiden Argumente ungerade,
dann kann dieser Fall niemals wieder eintreten (genau das ungerade Argument ist in allen
anderen Reduktionsfällen unveränderlich). Solange beide Argumente gerade sind, kann
man sie also kontinuierlich reduzieren, bis nach
gerade sind, kann man grundsätzlich aus der
Haupt-Iterationsschleife herausziehen. Denn wird einmal eines der beiden Argumente ungerade,
dann kann dieser Fall niemals wieder eintreten (genau das ungerade Argument ist in allen
anderen Reduktionsfällen unveränderlich). Solange beide Argumente gerade sind, kann
man sie also kontinuierlich reduzieren, bis nach  Schritten entweder
Schritten entweder 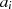 oder
oder  ungerade geworden ist. Danach kann auf
ungerade geworden ist. Danach kann auf 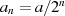 und
und 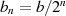 irgendein binärer
(erweiterter) GCD-Algorithmus angewendet werden, der
irgendein binärer
(erweiterter) GCD-Algorithmus angewendet werden, der 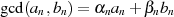 ermittelt.
ermittelt.
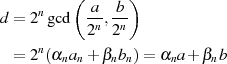
Der so ermittelte größte gemeinsame Teiler muß am Schluß nur noch mit 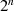 multipliziert werden (also um
multipliziert werden (also um  Bit verschoben), was auch Algorithmus 4 entsprechend
wiedergibt.44
Wir können deshalb in den Betrachtungen zum erweiterten binären GCD-Algorithmus (siehe
nächste Abschnitte) immer voraussetzen, daß
Bit verschoben), was auch Algorithmus 4 entsprechend
wiedergibt.44
Wir können deshalb in den Betrachtungen zum erweiterten binären GCD-Algorithmus (siehe
nächste Abschnitte) immer voraussetzen, daß  oder
oder  ungerade ist.
ungerade ist.
 oder
oder  ungerade ist (oder beide), kann man ausgehend von
ungerade ist (oder beide), kann man ausgehend von 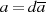 und
und 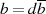 feststellen:45
feststellen:45
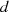 ist ungerade.
ist ungerade.
 ungerade sein, dann ist es dessen teilerfremde Anteil
ungerade sein, dann ist es dessen teilerfremde Anteil 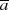 ebenfalls.
ebenfalls.
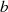 ungerade sein, dann ist es dessen teilerfremde Anteil
ungerade sein, dann ist es dessen teilerfremde Anteil 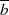 auch.
auch.
Algorithmus nach KALISKI46 [Kal95] Betrachtet man das Reduktionsschema des binären GCD-Algorithmus, so kann man verschiedenste lineare Transformationen der Art

definieren, wobei sich die einzelnen Betrachtungsweisen durch unterschiedliche Werte in den
Koeffizienten unterscheiden. Bei jedem Schritt sind so 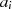 und
und 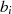 als lineare Funktion von
als lineare Funktion von 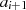 und
und
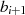 darstellbar, die Ausgangsgrößen
darstellbar, die Ausgangsgrößen 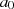 und
und 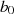 deshalb als lineare Funktionen von
deshalb als lineare Funktionen von 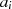 und
und 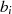 .
.
Durch Einsetzen von 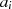 und
und  in folgende Gleichung,
in folgende Gleichung,

gefolgt von einem Koeffizientenvergleich, kann man für die konkreten Reduktionsfälle die jeweilige
Transformationen der Linearfaktoren ableiten (siehe Tabelle 4.2). Am Beispiel 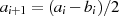 ,
,
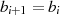 soll das Vorgehen exemplarisch verdeutlicht werden.
soll das Vorgehen exemplarisch verdeutlicht werden.

Aus den Transformationen nach Tabelle 4.2 kann man außerdem die Determinante
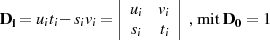
bestimmen.
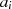 | 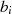 | 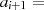 | 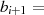 | 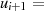 | 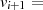 | 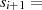 | 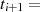 | 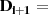 |
| gerade | 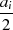 | 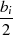 | 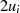 | 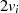 | 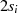 | 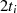 | 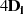 |
|
| gerade | ungerade |  | 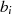 | 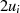 |  | 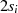 |  | 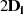 |
| ungerade | gerade | 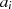 | 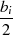 |  | 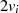 | 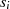 |  |  |
| ungerade, 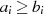 |  | 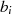 | 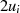 | 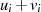 |  | 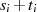 | 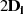 |
|
| ungerade, 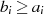 | 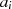 | 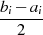 | 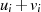 | 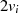 | 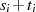 |  |  |
|
Um den Zusammenhang mit den BéZOUT-Koeffizienten 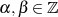 in
in 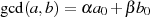 herzustellen, stellen wir die Formeln 4.6 und 4.7 nach
herzustellen, stellen wir die Formeln 4.6 und 4.7 nach 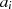 und
und 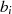 um. Dazu werden beide
Gleichungen mit den Linearfaktoren der jeweils anderen multipliziert und dann wechselweise
voneinander subtrahiert.
um. Dazu werden beide
Gleichungen mit den Linearfaktoren der jeweils anderen multipliziert und dann wechselweise
voneinander subtrahiert.

Schließt man den Fall aus, daß  und
und 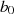 gerade sind (
gerade sind (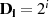 , vgl. Anmerkungen auf Seite 92),
dann kann für den letzten Iterationsschritt
, vgl. Anmerkungen auf Seite 92),
dann kann für den letzten Iterationsschritt 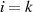 , in Abhängigkeit davon ob
, in Abhängigkeit davon ob 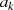 oder
oder 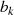 zuerst
verschwindet, folgendermaßen konkretisiert werden:
zuerst
verschwindet, folgendermaßen konkretisiert werden:

An diesem Punkt stellen wir jedoch fest, daß es sich bei den Größen  ,
, 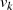 ,
, 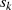 und
und 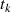 nicht um
die Kofaktoren von
nicht um
die Kofaktoren von 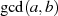 , sondern um eine Linearfaktordarstellung von
, sondern um eine Linearfaktordarstellung von  handelt.47
handelt.47
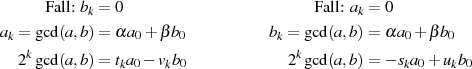
Um aus 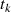 ,
,  und
und 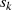 ,
, 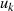 die BéZOUT-Koeffizienten
die BéZOUT-Koeffizienten  und
und 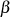 zu bestimmen, sind zusätzliche
Korrekturschritte nötig, welche in [Kal95] auch Korrekturphase (oder Phase II) genannt werden.
Ziel ist es dabei, die rechte Seite der letzten Gleichung durch
zu bestimmen, sind zusätzliche
Korrekturschritte nötig, welche in [Kal95] auch Korrekturphase (oder Phase II) genannt werden.
Ziel ist es dabei, die rechte Seite der letzten Gleichung durch 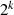 zu dividieren (oder in
zu dividieren (oder in 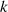 Schritten wiederholt durch 2). Da die linke Seite immer eine gerade Zahl ist, können folgende
Schlußfolgerungen im Falle
Schritten wiederholt durch 2). Da die linke Seite immer eine gerade Zahl ist, können folgende
Schlußfolgerungen im Falle 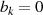 gezogen werden (falls
gezogen werden (falls 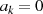 war, äquivalent für
war, äquivalent für 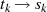 und
und
 ):48
):48
 und
und  gerade, dann ist eine ganzzahlige Halbierung
gerade, dann ist eine ganzzahlige Halbierung 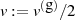 ,
, 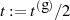 möglich (d. h. führt wieder zu einer ganzen Zahl).
möglich (d. h. führt wieder zu einer ganzen Zahl).
 bzw.
bzw.  ungerade) kann man wegen
ungerade) kann man wegen

die Reduktion 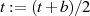 bzw.
bzw. 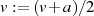 vornehmen, ohne daß sich die
Gleichung ändert. Man wandelt jedoch die ungerade Zahl
vornehmen, ohne daß sich die
Gleichung ändert. Man wandelt jedoch die ungerade Zahl  bzw.
bzw.  in eine gerade Zahl,
die dann (wie gewünscht) durch
in eine gerade Zahl,
die dann (wie gewünscht) durch  teilbar ist. Die Ursache liegt einerseits darin begründet,
daß die linke (und demzufolge auch rechte) Seite der Gleichung
teilbar ist. Die Ursache liegt einerseits darin begründet,
daß die linke (und demzufolge auch rechte) Seite der Gleichung
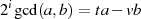
immer eine gerade Zahl repräsentiert und andererseits, entweder  oder/und
oder/und  als ungerade
vorausgesetzt wurden. Berücksichtigt man die folgenden Gesetzmäßigkeiten:
als ungerade
vorausgesetzt wurden. Berücksichtigt man die folgenden Gesetzmäßigkeiten:
dann sind genau drei Fälle konstruierbar, in denen  oder
oder  ungerade ist.
ungerade ist.
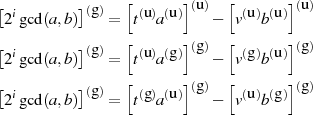
In allen diesen Varianten führt aber die Addition  bzw.
bzw.  zu einer geraden Zahl, womit
sich das Korrekturverfahren bestätigt.
zu einer geraden Zahl, womit
sich das Korrekturverfahren bestätigt.
 nach KALISKI
nach KALISKI ungerade
ungerade 
 ungerade
{Phase I}
ungerade
{Phase I}
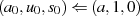
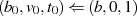
 {Flag, daß anzeigt, ob schlußendlich
{Flag, daß anzeigt, ob schlußendlich  oder
oder  negativ
ist}
negativ
ist}

 do
do
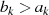 then
then
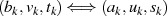 {gewährleistet
{gewährleistet
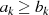 }
}
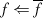 {invertiere
Flag}
{invertiere
Flag}
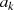 ungerade
ungerade 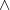
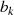 ungerade then
ungerade then
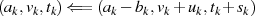 {
{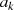 ist jetzt gerade,
ist jetzt gerade, 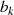 weiterhin
ungerade}
weiterhin
ungerade}
 gerade then
gerade then
 {
{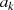 gerade,
gerade, 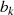 ungerade}
ungerade}
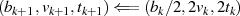 {
{ ungerade,
ungerade, 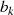 gerade}
gerade}
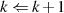
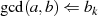 {Teilergebnis
{Teilergebnis
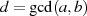 }
{Phase II}
}
{Phase II}

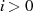 do
do
 ungerade
ungerade 
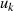 ungerade then
ungerade then
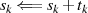 {Addition von
{Addition von 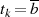 (vgl.
Bemerkung 3)}
(vgl.
Bemerkung 3)}
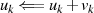 {Addition von
{Addition von 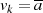 (vgl.
Bemerkung 3)}
(vgl.
Bemerkung 3)}
 {Korrektur
{Korrektur
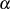 }
}
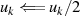 {Korrektur
{Korrektur
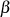 }
}

 {Wenn
{Wenn 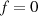 , dann
, dann 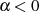 , sonst
, sonst
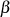 }
}
Als Ergebnis kann man Algorithmus 5 formulieren, wobei außerdem folgende Anmerkungen berücksichtigt wurden:

schlußfolgern, d. h. bei 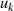 und
und  handelt es sich im Fall
handelt es sich im Fall 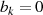 (gleichermaßen für
(gleichermaßen für 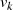 ,
, 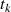 im
Fall
im
Fall 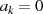 ) um die teilerfremden Faktoren
) um die teilerfremden Faktoren

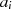 oder
oder  müssen die Linearfaktoren
müssen die Linearfaktoren 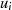 ,
, 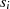 ,
, 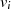 und
und 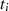 in
Phase I schrittweise anwachsen, denn nur so können
in
Phase I schrittweise anwachsen, denn nur so können  und
und 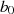 nach Gleichung 4.6 und 4.7
konstant bleiben. In [Kal95, Theorem 1] wird bewiesen, daß keine dieser Größen
während der Ausführung des Algorithmus den Maximalwert
nach Gleichung 4.6 und 4.7
konstant bleiben. In [Kal95, Theorem 1] wird bewiesen, daß keine dieser Größen
während der Ausführung des Algorithmus den Maximalwert 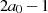 überschreitet (für
überschreitet (für
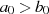 ).49
).49
 bzw.
bzw.  kann (entsprechend
Anmerkung 5 auf Seite 94) ersetzt werden durch eine Addition von
kann (entsprechend
Anmerkung 5 auf Seite 94) ersetzt werden durch eine Addition von 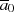 bzw.
bzw.
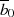 .50
.50
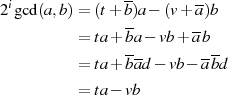
Algorithmus nach PENK [Knu98, Exercise 4.5.2.39], [MvV92, 14.4.3]
Dieser Algorithmus stellt 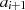 und
und  als lineare Funktion von
als lineare Funktion von 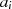 und
und 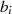 dar, letztlich wird also
von
dar, letztlich wird also
von 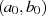 auf
auf 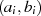 geschlossen.
geschlossen.
Vorteilhaft wirkt sich aus, daß im letzten Reduktionsschritt (wenn 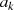 oder
oder 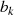 verschwindet)
verschwindet)
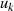 und
und 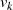 bzw.
bzw. 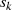 und
und 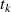 direkt die gesuchten BéZOUT-Kofaktoren
direkt die gesuchten BéZOUT-Kofaktoren  ,
, 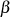 darstellen.
darstellen.

Durch Einsetzen von 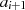 und
und 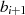 (entsprechend Tabelle 4.1) in die Gleichungen
(entsprechend Tabelle 4.1) in die Gleichungen
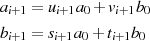
kann man für den jeweiligen Reduktionsfall die zugehörige Transformationen der Linearfaktoren
ableiten. Wieder am Beispiel 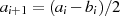 ,
, 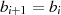 soll das Vorgehen veranschaulicht werden
(
soll das Vorgehen veranschaulicht werden
(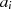 und
und 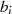 sind ungerade,
sind ungerade, 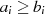 ).
).
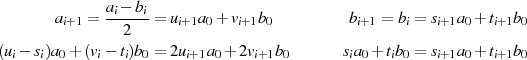
Vergleich von linker und rechter Seite läßt den Schluß zu:

Die anderen Kombinationen können genau nach demselben Schema abgeleitet werden. Tabelle 4.3 faßt die Ergebnisse in übersichtlicher Form zusammen.51
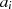 | 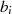 | 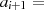 | 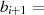 | 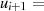 | 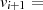 | 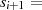 | 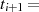 |
| gerade | ungerade | 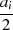 | 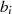 | 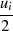 |  | 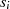 | 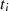 |
| ungerade | gerade | 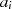 | 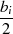 | 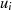 |  | 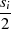 | 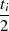 |
| ungerade, 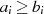 | 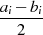 | 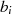 | 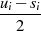 | 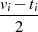 |  | 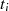 |
|
| ungerade, 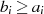 | 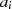 | 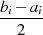 | 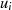 | 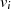 |  | 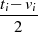 |
|
Dabei tritt allerdings wieder das bekannte Problem auf: Wie kann man die Ganzzahligkeit des jeweiligen Linearfaktoren bei der Halbierung wahren? Die Antwort haben wir schon beim vorangegangenen Algorithmus geliefert – indem die Ausgangsgleichungen 4.8 und 4.9 folgendermaßen erweitert:
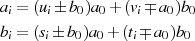
und dadurch ungerade Zahlen 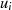 ,
, 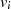 bzw.
bzw.  ,
, 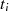 in gerade umwandelt.
in gerade umwandelt.
Beschränken wir uns auf die Kombinationen nach Tabelle 4.3, in denen  und
und 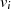 verändert werden
(äquivalent für
verändert werden
(äquivalent für  und
und  ). Für den Fall, daß
). Für den Fall, daß 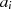 gerade und
gerade und 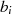 ungerade ist (zweite Zeile in
4.3), können wir auf die Argumentation von Seite 100 zurückgreifen (Phase II der Methode nach
KALISKI). Sie erlaubt uns die Subtraktion/Addition von
ungerade ist (zweite Zeile in
4.3), können wir auf die Argumentation von Seite 100 zurückgreifen (Phase II der Methode nach
KALISKI). Sie erlaubt uns die Subtraktion/Addition von 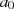 und
und  für den Fall, daß
für den Fall, daß 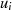 oder
oder 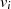 ungerade ist. Die Situation, daß
ungerade ist. Die Situation, daß  und
und 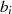 ungerade sind (vorletzte Zeile in 4.3), kann man durch
gedankliche Verzögerung der Halbierung in den nächsten Iterationsschritt erklären. Wählt man als
modifizierten Einzelschritt
ungerade sind (vorletzte Zeile in 4.3), kann man durch
gedankliche Verzögerung der Halbierung in den nächsten Iterationsschritt erklären. Wählt man als
modifizierten Einzelschritt 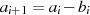 (und entsprechend
(und entsprechend 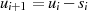 ,
,  ), so
reduziert sich die Fragestellung wieder auf eine gerade Zahl
), so
reduziert sich die Fragestellung wieder auf eine gerade Zahl 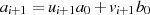 , also auf den
vorangegangenen Fall.
, also auf den
vorangegangenen Fall.
Als Ergebnis der Ausführungen kann man Algorithmus 6 formulieren. Der Vorteil des Algorithmus (gegenüber KALISKI’s) liegt vor allem darin, daß keine Korrekturphase nötig ist. Nachteilig für eine praktische Umsetzung ist die notwendige Vorzeichen-Arithmetik.
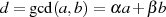 nach PENK
nach PENK