


Um von einem Restklassenring 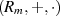 sprechen zu können ist der Nachweis aller Ringaxiome von
Abschnitt 1.2 in Bezug auf die Menge der Restklassen
sprechen zu können ist der Nachweis aller Ringaxiome von
Abschnitt 1.2 in Bezug auf die Menge der Restklassen 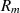 notwendig [Wel01, 5.]. Dazu geht man
von der Modulo-Arithmetik nach Gleichung 3.1 und 3.2 aus und prüft jeden Punkt durch
Einzelbetrachtung:
notwendig [Wel01, 5.]. Dazu geht man
von der Modulo-Arithmetik nach Gleichung 3.1 und 3.2 aus und prüft jeden Punkt durch
Einzelbetrachtung:
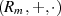 eine ABEL’sche Gruppe bilden, d. h.
eine ABEL’sche Gruppe bilden, d. h.
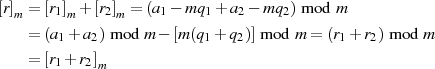
![[r ] + ([r ] + [r ] )= ([r] + [r] )+ [r] = [r ] + [r] + [r]
1m 2m 3 m 1 m 2m 3m 3 m 2 m 1m](algebra545x.png)
![e(+) = [0]m = mq0](algebra546x.png) existiert;
existiert;
![[r]m + [0]m = (a− mq + mq0) mod m = [a − m (q− q0)] mod m = a mod m = [r]m](algebra547x.png)
![− [r]m = (m − a) mod m](algebra548x.png) mit
mit
![[r]m+ (− [r]m )= a mod m + (m − a) mod m = m mod m = [0]m.](algebra549x.png)
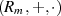 eine Halbgruppe darstellen, also
eine Halbgruppe darstellen, also
![[r]m ∈ Rm](algebra554x.png) das Distributivgesetz erfüllt sein.
das Distributivgesetz erfüllt sein.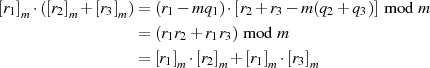
Da 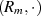 ein neutrales Element
ein neutrales Element 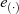 mit
mit ![[r]m ⋅e(⋅) = [r]m](algebra558x.png) besitzt, handelt es sich sogar um einen
Ring mit Eins.
besitzt, handelt es sich sogar um einen
Ring mit Eins.
![[r] ⋅[1] = (r⋅1) mod m = r mod m = [r]
m m m](algebra559x.png)
Aus Anwendungssicht ist sofort zu erkennen, daß insbesondere die Restklassen 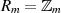 alle diese
Bedingungen für
alle diese
Bedingungen für 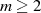 erfüllen und somit einen kommutativen Ring mit Einselement
bilden.
erfüllen und somit einen kommutativen Ring mit Einselement
bilden.