


Jeder endliche Körper ist durch eine beschränkte Anzahl von Elementen gekennzeichnet, auf welche die
Körperaxiome von Abschnitt 1.3 zutreffen. Man nennt solche algebraischen Strukturen auch GALOIS-Körper
und bezeichnet sie mit 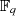 oder
oder 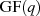 , wobei
, wobei 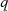 die Ordnung (Anzahl der Elemente) des Körpers
angibt.16
Bei der Konstruktion eines endlichen Körpers ist von allergrößter Bedeutung, daß zu den Eigenschaften
eines Ringes noch die der multiplikativen Gruppe kommen. Zusätzliches Kriterium ist danach die
Existenz des multiplikativ inversen Elements
die Ordnung (Anzahl der Elemente) des Körpers
angibt.16
Bei der Konstruktion eines endlichen Körpers ist von allergrößter Bedeutung, daß zu den Eigenschaften
eines Ringes noch die der multiplikativen Gruppe kommen. Zusätzliches Kriterium ist danach die
Existenz des multiplikativ inversen Elements 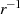 zu jedem
zu jedem 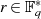 .
.
Definiert 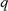 die Anzahl der Elemente im Körper, d. h. inklusive Nullelement
die Anzahl der Elemente im Körper, d. h. inklusive Nullelement 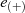 , dann muß für die
Ordnung der multiplikativen Gruppe
, dann muß für die
Ordnung der multiplikativen Gruppe 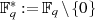 gelten:
gelten:
Entsprechend Abschnitt 2.1.3 muß die Ordnung der multiplikativen Gruppe ein Vielfaches der
Elementeordnung 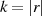 sein:
sein: 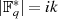 (Satz von LAGRANGE). Ein GALOIS-Körper
kann deshalb nicht jede beliebige Ordnung annehmen – wegen vorgenannter Bedingung
müssen
(Satz von LAGRANGE). Ein GALOIS-Körper
kann deshalb nicht jede beliebige Ordnung annehmen – wegen vorgenannter Bedingung
müssen 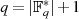 und die Ordnung
und die Ordnung 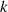 eines jeden Elements
eines jeden Elements 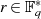 teilerfremd
sein.17
teilerfremd
sein.17
Diese Erkenntnis läßt sich (einerseits logisch, aber auch rein analytisch) aus
mit Hilfe des Satzes von BéZOUT ableiten. Dazu vergleicht man Beziehung 42 mit Formel 4.3 aus Abschnitt 4.1.1 und stellt fest:
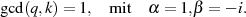
Die einfachste Möglichkeit Teilerfremdheit zu gewährleisten, ist die Wahl von 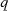 als Primzahl oder als
Potenz einer Primzahl. Im ersten Fall nennt man
als Primzahl oder als
Potenz einer Primzahl. Im ersten Fall nennt man 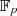 einen Primzahlenkörper, für
einen Primzahlenkörper, für 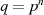 einen
Erweiterungs- oder Binärkörper (weitere Ausführungen zu
einen
Erweiterungs- oder Binärkörper (weitere Ausführungen zu 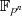 in Abschnitt 3.4).
in Abschnitt 3.4).
Aus Abschnitt 2.1.5 (Gleichung 2.14) ist bekannt, daß man die Elemente der multiplikativen Gruppe
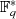 als Nullstellen des Polynoms
als Nullstellen des Polynoms 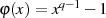 auffassen kann. Nimmt man jetzt noch das
Nullelement
auffassen kann. Nimmt man jetzt noch das
Nullelement 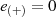 hinzu, dehnt also die Betrachtung von der multiplikativen Gruppe
auf alle Elemente des Körpers aus, dann kann man als zusätzlichen Linearfaktor
hinzu, dehnt also die Betrachtung von der multiplikativen Gruppe
auf alle Elemente des Körpers aus, dann kann man als zusätzlichen Linearfaktor 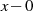 einbeziehen:
einbeziehen:
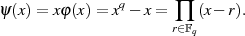 | (2.19) |
Deshalb bilden die Nullstellen von 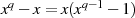 einen endlichen Körper
einen endlichen Körper 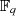 .
.