


Ausgehend von der eindimensionalen Transformation einer Zufallsgröße (im vorherigen Abschnitt) läßt sich das Problem von Funktionen mehrdimensionaler Zufallsgrößen wiefolgt formulieren:
|
Gesucht ist die Wahrscheinlichkeitsdichte 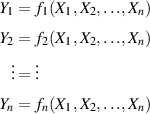 ergibt. |
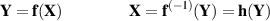 | (34) |
ein, dann wird schon auf Symbolebene die Ähnlichkeit zum eindimensionalen Fall
erkennbar. Aus diesem Grund wird hier der Ansatz der formalen Erweiterung von
Gleichung 30 auf  Dimensionen verfolgt, wobei wir (zuerst) jegliche Betragszeichen
ignorieren.15
Dimensionen verfolgt, wobei wir (zuerst) jegliche Betragszeichen
ignorieren.15
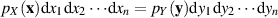 | (35) |
Dabei kann man sich weiterhin von der anschaulichen Darstellung in Abbildung 2 leiten lassen, muß
die Transformation von eindimensionalen, differentiellen Größen (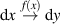 ) nun aber auf Gebiete der
Dimension
) nun aber auf Gebiete der
Dimension  ausdehnen (
ausdehnen (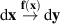 ).
).
Den Zusammenhang zwischen den
Inhaltsmomenten16
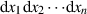 und
und 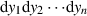 gibt uns die aus der Integralrechnung bekannte Funktional- bzw. JACOBI-Determinante
gibt uns die aus der Integralrechnung bekannte Funktional- bzw. JACOBI-Determinante
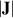 .17
.17
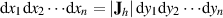 | (36) |
Die ihr zugrunde liegende JACOBI-Matrix hat eine 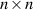 Struktur, in der jedes Element die partielle
Ableitung der Funktion
Struktur, in der jedes Element die partielle
Ableitung der Funktion 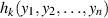 nach einer Variablen
nach einer Variablen 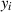 enthält. Für den Funktionsvektor
enthält. Für den Funktionsvektor 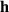 hat sie das folgende Aussehen:
hat sie das folgende Aussehen:
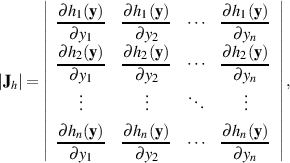
wobei wir die Betragszeichen sowohl als Kennzeichnung für eine Determinante als auch den echten
Betrag des Ergebnisses werten wollen. Vergleicht man nun Formel 35 und 36, dann wird der
Zusammenhang zwischen den Wahrscheinlichkeitsdichten von 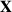 und
und 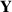 sofort offensichtlich [PP02,
6], [Ros04, 2.5], [Gne58, § 23].
sofort offensichtlich [PP02,
6], [Ros04, 2.5], [Gne58, § 23].
Die ebenfalls interessante Verteilungsfunktion von 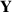 kann man z. B. aus Definitionsgleichung 17 durch Einsetzen von
Formel 35 gewinnen.18
kann man z. B. aus Definitionsgleichung 17 durch Einsetzen von
Formel 35 gewinnen.18
Die Integrationsgrenzen ergeben sich dabei aus der Bedingung  für das
Integrationsgebiet
für das
Integrationsgebiet 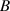 (vgl. Definition der Verteilungsfunktion:
(vgl. Definition der Verteilungsfunktion: 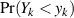 ).
).
Auf der Grundlage von Formel 35 lassen sich nun auch die Erwartungswerte 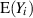 berechnen.
berechnen.
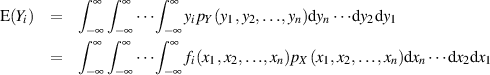
Für den zweidimensionalen Spezialfall 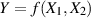 bestimmt sich der Erwartungswert
wiefolgt:
bestimmt sich der Erwartungswert
wiefolgt:
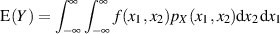 | (39) |