


Schon C.G.J. JACOBI hat in [Jac29] nachgewiesen, daß Lösungen der Differentialgleichung 70
algebraische Funktionen der Form 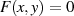 sein können [Tri48, IV], [Hur00, II-5, § 4 ff.]. Für die
implizite Darstellung solcher Funktionen wiefolgt
sein können [Tri48, IV], [Hur00, II-5, § 4 ff.]. Für die
implizite Darstellung solcher Funktionen wiefolgt
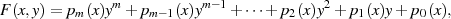 | (72) |
wobei 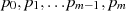 Polynome in
Polynome in  sind, kann bekanntermaßen in bestimmten Spezialfällen
eine explizite Lösungsformel
sind, kann bekanntermaßen in bestimmten Spezialfällen
eine explizite Lösungsformel  ermittelt werden. Bei dem gesuchten Integral
ermittelt werden. Bei dem gesuchten Integral 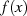 handelt es
sich in den einfachsten Fällen um eine irrationale (
handelt es
sich in den einfachsten Fällen um eine irrationale ( ) oder rationale Funktion (
) oder rationale Funktion ( ), wobei
sich Letztere als
), wobei
sich Letztere als
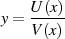 | (73) |
mit den Polynomen
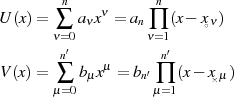
darstellen läßt.24
Um für diesen Funktionstyp den Nachweis zu erbringen, daß es sich um eine Lösung von
Differentialgleichung 70 handelt, folgen wir [Cay76, § 218 ff.] und setzten zuerst 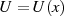 bzw.
bzw.
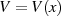 und bilden dann
und bilden dann 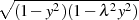 sowie die Ableitung
sowie die Ableitung 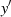 .
.
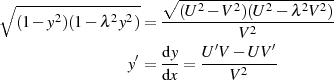
Dividiert man die Ableitung 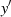 durch
durch  entsteht der Ausdruck
entsteht der Ausdruck
welcher ja letztlich der rechten Seite von Gleichung 69 (multipliziert mit  ) entsprechen
soll.
) entsprechen
soll.

Notwendige Voraussetzung dafür ist zuerst einmal, daß für den Grad der Polynome
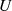 und
und 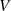 die Einschränkung
die Einschränkung 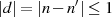 gilt, d. h. entweder beide Polynome
sind vom Grad
gilt, d. h. entweder beide Polynome
sind vom Grad  (bzw.
(bzw. 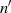 ) oder eines ist vom Grade
) oder eines ist vom Grade  , das andere aber
, das andere aber
 .25
.25
Beweis. Der Nachweis basiert auf der letzten Gleichung in folgender Darstellung
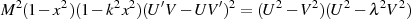
und vergleicht einfach den Grad von links- und rechtsseitigem Polynom (mit entsprechender Fallunterscheidung).
Eine Funktion ist also vom Grad  , die andere vom Grad
, die andere vom Grad  und deshalb die Differenz
und deshalb die Differenz
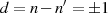 . Allerdings ergeben sich dieselben Verhältnisse auch für
. Allerdings ergeben sich dieselben Verhältnisse auch für 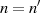 (also
(also 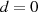 ), denn
in diesem Fall verschwindet der höchstwertige Koeffizient (mit Wert
), denn
in diesem Fall verschwindet der höchstwertige Koeffizient (mit Wert 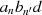 ) in
) in  .
Verringert man entsprechend den linksseitigen Grad in Gleichung 75 um Eins (auf der rechten Seite
bleibt alles wie gehabt), dann wird sofort erkennbar, daß auch
.
Verringert man entsprechend den linksseitigen Grad in Gleichung 75 um Eins (auf der rechten Seite
bleibt alles wie gehabt), dann wird sofort erkennbar, daß auch 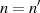 eine Lösungsmöglichkeit
ist. __
eine Lösungsmöglichkeit
ist. __
Nimmt man nun an, daß sich in Gleichung 74 ein Faktor  vom Ausdruck
vom Ausdruck 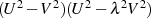 abspalten läßt, dann ist der Term
abspalten läßt, dann ist der Term  in
in  ebenfalls als Faktor enthalten.
ebenfalls als Faktor enthalten.
Beweis. Ist 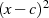 ein Faktor (
ein Faktor ( eine doppelte Nullstelle) von
eine doppelte Nullstelle) von  oder
oder 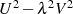 ,
dann ist
,
dann ist 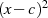 auch ein Faktor von
auch ein Faktor von  oder
oder  bzw.
bzw.  oder
oder 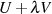 .
Betrachten wir im weiteren nur den Fall, daß der Faktor
.
Betrachten wir im weiteren nur den Fall, daß der Faktor 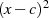 in
in  enthalten ist
(gleiches gilt für die anderen Fälle). Es ergeben sich dann die Darstellungen
enthalten ist
(gleiches gilt für die anderen Fälle). Es ergeben sich dann die Darstellungen
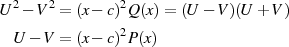
mit den Ableitungen nach 

Bildet man jetzt
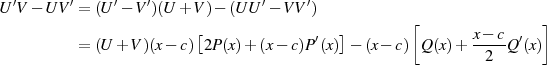
dann bestätigt das gemeinsame Vorkommen des Faktors  in allen Summanden unsere
Annahme. __
in allen Summanden unsere
Annahme. __
Setzt man eine solche Abspaltung für alle  Wurzeln von
Wurzeln von  fort, dann bleibt in
fort, dann bleibt in
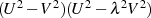 , dessen Grad ja
, dessen Grad ja 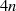 ist, ein Produktterm vom Grad
ist, ein Produktterm vom Grad 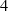 übrig, der nicht
mehr gekürzt werden kann. Mit den konstanten Koeffizienten
übrig, der nicht
mehr gekürzt werden kann. Mit den konstanten Koeffizienten 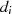 ergibt sich demzufolge die
Darstellung:26
ergibt sich demzufolge die
Darstellung:26

Kehrt man mit diesen Formeln zurück zur Ausgangsgleichung 74
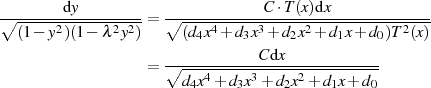
und berücksichtigt außerdem, daß eine Überführung des besagten Produktterms in die Form
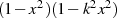 immer möglich ist (siehe [Tri48, II, § 3], [WW27, §
immer möglich ist (siehe [Tri48, II, § 3], [WW27, § 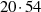 , §
, §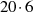 ]), dann ist mit
einer rationalen Polynomfunktion
]), dann ist mit
einer rationalen Polynomfunktion 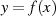 die elliptische Transformation nach Gleichung 70
möglich.27
Aus dieser Feststellung heraus kann man bezüglich der Bestimmung der Koeffizienten von
die elliptische Transformation nach Gleichung 70
möglich.27
Aus dieser Feststellung heraus kann man bezüglich der Bestimmung der Koeffizienten von 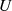 und
und 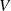 noch die Bedingung
noch die Bedingung
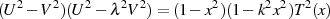
formulieren.