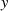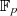
Das Bestimmen der Quadratwurzel kann man im Körper 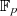 recht effizient mit dem TONELLI-SHANKS
Algorithmus erledigen. Bevor man aber dazu übergehen kann den Algorithmus zu erläutern, muß man
sich unbedingt über einige Fakten in Bezug auf das Quadrieren von Körperelementen klar werden.
Ohne wesentlich an Allgemeinheit zu verlieren, betrachten wird dazu die multiplikative
Gruppe
recht effizient mit dem TONELLI-SHANKS
Algorithmus erledigen. Bevor man aber dazu übergehen kann den Algorithmus zu erläutern, muß man
sich unbedingt über einige Fakten in Bezug auf das Quadrieren von Körperelementen klar werden.
Ohne wesentlich an Allgemeinheit zu verlieren, betrachten wird dazu die multiplikative
Gruppe 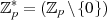 und formulieren zuerst die folgenden Grundaussagen in Bezug
auf:60
und formulieren zuerst die folgenden Grundaussagen in Bezug
auf:60
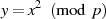
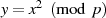 ersieht man sofort, daß immer zwei Elemente
ersieht man sofort, daß immer zwei Elemente 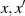 genau zum selben
genau zum selben 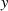 führen – ein „Positives“ und ein „Negatives“:
führen – ein „Positives“ und ein „Negatives“: 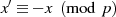 .
.
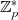 genau
genau 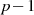 Elemente enthält (besitzt die Ordnung
Elemente enthält (besitzt die Ordnung 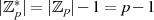 ),
können
),
können 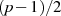 Elemente
Elemente 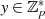 keine Quadratwurzel besitzen. Denn umgekehrt
betrachtet sind ja die verfügbaren
keine Quadratwurzel besitzen. Denn umgekehrt
betrachtet sind ja die verfügbaren 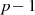 Elemente
Elemente  wegen der Paarbildung beim
Quadrieren (welche zu
wegen der Paarbildung beim
Quadrieren (welche zu 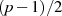 Elementen
Elementen 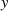 führt) schon „aufgebraucht“.
führt) schon „aufgebraucht“.
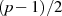 Elemente
Elemente 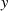 , welche der Beziehung
, welche der Beziehung 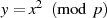 genügen, gilt
wegen des kleinen Satzes von FERMAT (vgl. Abschnitt 3.3.2):
genügen, gilt
wegen des kleinen Satzes von FERMAT (vgl. Abschnitt 3.3.2):
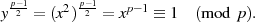 | (4.19) |
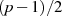 Elemente
Elemente 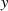 , welche keine zugeordnete Quadratwurzel
, welche keine zugeordnete Quadratwurzel  besitzen, gilt
hingegen:61
besitzen, gilt
hingegen:61
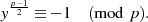 | (4.20) |
Für einen kurzen Beweis nehmen wir uns ein bestimmtes (konstantes) Element 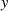 heraus und
betrachten die Zerlegung
heraus und
betrachten die Zerlegung 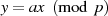 , welche es in
, welche es in 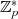 immer geben muß:
immer geben muß:
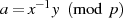 . Wenn man nun für
. Wenn man nun für  alle möglichen Werte
alle möglichen Werte 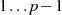 setzt, dann muß
auch
setzt, dann muß
auch  entsprechend variieren. Wegen:
entsprechend variieren. Wegen:
in 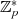 wird
wird  einerseits alle möglichen Werte
einerseits alle möglichen Werte 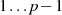 annehmen und andererseits wird jedes
Produkt
annehmen und andererseits wird jedes
Produkt  insofern doppelt vorkommen, daß
insofern doppelt vorkommen, daß  und
und  nur die Rolle getauscht haben. In
Abbildung 4.1 sind mögliche Produkte für
nur die Rolle getauscht haben. In
Abbildung 4.1 sind mögliche Produkte für 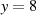 (hat keine Wurzel) und
(hat keine Wurzel) und 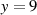 (Wurzeln sind
(Wurzeln sind
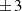 ) beispielhaft in
) beispielhaft in 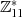 dargestellt (wobei gestrichelte Linien Produkte kennzeichnen, bei
denen
dargestellt (wobei gestrichelte Linien Produkte kennzeichnen, bei
denen  und
und  nur die Rolle getauscht haben).
nur die Rolle getauscht haben).
Multiplizieren wir alle Produkte  miteinander und schließen dabei die Doppelungen aus (d. h.
berücksichtigen nur die Produkte in Abbildung 4.1a, welche mit durchgezogenen Linien
dargestellt sind), dann hat man alle Elemente
miteinander und schließen dabei die Doppelungen aus (d. h.
berücksichtigen nur die Produkte in Abbildung 4.1a, welche mit durchgezogenen Linien
dargestellt sind), dann hat man alle Elemente 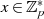 miteinander multipliziert.
miteinander multipliziert.
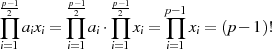
Bei den 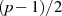 Produkten
Produkten 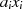 handelt es sich aber genau um die Potenz
handelt es sich aber genau um die Potenz
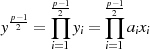
und so kann man mit dem Satz von WILSON (siehe Formel 3.7) den Beweis abschließen:
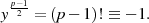
Noch bevor man also versucht die Quadratwurzel 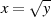 zu berechnen, kann man mit Hilfe des
gerade eingeführten (EULER-) Kriteriums prüfen, ob diese überhaupt existiert. Die Nomenklatur für das
EULER-Kriterium stammt allerdings von A.-M. LEGENDRE und wird als LEGENDRE-Symbol
bezeichnet:
zu berechnen, kann man mit Hilfe des
gerade eingeführten (EULER-) Kriteriums prüfen, ob diese überhaupt existiert. Die Nomenklatur für das
EULER-Kriterium stammt allerdings von A.-M. LEGENDRE und wird als LEGENDRE-Symbol
bezeichnet:
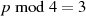
Im speziellen Fall 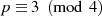 kann man eine sehr einfache Lösung für die Quadratwurzel
kann man eine sehr einfache Lösung für die Quadratwurzel
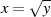 erhalten, sofern sie denn existiert [Ros99, Theorem 9.3], [ANS05, D.1.4]:
erhalten, sofern sie denn existiert [Ros99, Theorem 9.3], [ANS05, D.1.4]:
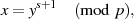 | (4.22) |
mit 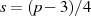 .
.
Ausgangspunkt für einen kurzen Beweis könnte die folgende Darstellung für das Modul 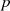 sein:62
sein:62
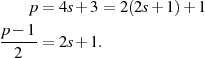
Wird sie im Zusammenhang mit dem EULER-Kriterium von Gleichung 4.19 angewendet, dann bestätigt sich Formel 4.22 wiefolgt:
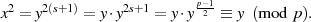
Idee
Der TONELLI-SHANKS Algorithmus nach [Ton91, Sha73] reduziert, ausgehend von einem
Anfangswert 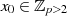 , den Exponenten
, den Exponenten 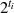 im Ausdruck
im Ausdruck
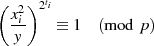 | (4.23) |
immer weiter, bis schließlich 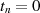 wird und deshalb
wird und deshalb 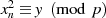 die gesuchte Lösung darstellt
(siehe z. B. auch [NZM91, 2.9], [CP05, 2.3.2]). Mit
die gesuchte Lösung darstellt
(siehe z. B. auch [NZM91, 2.9], [CP05, 2.3.2]). Mit 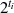 soll es sich aber nicht um irgendeine
Zweierpotenz handeln, sondern um die Ordnung des Elements
soll es sich aber nicht um irgendeine
Zweierpotenz handeln, sondern um die Ordnung des Elements 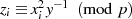 .
.
Es gilt also einen Algorithmus zu beschreiben, bei dem sowohl für den Startwert 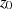 als auch für alle
Werte
als auch für alle
Werte 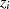 in
in
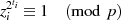 | (4.24) |
die Ordnung 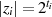 einerseits (und überhaupt) eine Zweierpotenz ist und andererseits (auch noch)
abnimmt.63
einerseits (und überhaupt) eine Zweierpotenz ist und andererseits (auch noch)
abnimmt.63
Startwerte Als Anfangswerte setzt man:

Dabei entspricht der Wert 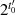 nicht zwingendermaßen der Ordnung
nicht zwingendermaßen der Ordnung 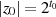 , er befriedigt aber
Kongruenz 4.24 grundsätzlich:
, er befriedigt aber
Kongruenz 4.24 grundsätzlich:
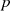 um eine Primzahl mit
um eine Primzahl mit 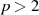 handeln soll (
handeln soll (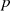 ist zwingendermaßen
ungerade), kann man
ist zwingendermaßen
ungerade), kann man
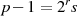 | (4.25) |
setzen (mit 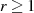 , maximal) und erhält so:
, maximal) und erhält so:
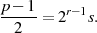
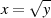 wirklich existieren (wovon wir ausgehen) dann gilt mit dem
EULER-Kriterium 4.21:
wirklich existieren (wovon wir ausgehen) dann gilt mit dem
EULER-Kriterium 4.21:
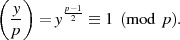
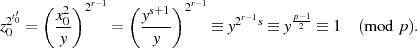 | (4.26) |
Interpretieren wir Kongruenz 4.26 jetzt mit dem Wissen aus Abschnitt 2.1.2, dann muß es sich bei 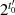 entweder um die Ordnung
entweder um die Ordnung 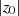 selbst oder aber um ein Vielfaches davon handeln:
selbst oder aber um ein Vielfaches davon handeln: 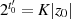 .
Deshalb können
.
Deshalb können 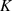 und
und 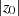 nur Zweierpotenzen sein (was
nur Zweierpotenzen sein (was 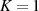 nicht ausschließt), d. h. für die
Ordnung kann man ohne weitere Bedenken
nicht ausschließt), d. h. für die
Ordnung kann man ohne weitere Bedenken 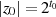 ansetzen (mit
ansetzen (mit 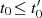 ). Um nun aus
). Um nun aus 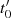 den
exakten Exponenten
den
exakten Exponenten 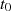 bzw. die Ordnung
bzw. die Ordnung 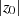 zu ermitteln, kann man
zu ermitteln, kann man 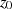 einfach so oft
quadrieren bis (nach FERMAT’s kleinem Satz) die Bedingung
einfach so oft
quadrieren bis (nach FERMAT’s kleinem Satz) die Bedingung 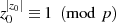 erfüllt
ist.
erfüllt
ist.
Iteration
Bevor wir zum iterativen Teil des Algorithmus übergehen können, benötigen wir noch die Mithilfe
irgendeines (zufällig gewählten) Elements 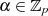 , welches keine Wurzel in
, welches keine Wurzel in 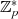 haben darf. Für
haben darf. Für 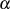 muß das EULER-Kriterium 4.21 dann den Wert
muß das EULER-Kriterium 4.21 dann den Wert
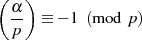
annehmen. Aus diesem Element 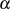 erzeugen wir ein neues Element
erzeugen wir ein neues Element 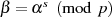 mit den
Eigenschaften:
mit den
Eigenschaften:
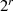 ergibt sich mit FERMAT’s kleinem Satz:
ergibt sich mit FERMAT’s kleinem Satz:
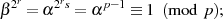
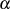 läßt sich schlußfolgern:
läßt sich schlußfolgern:
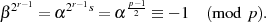 | (4.27) |
Nun wird die Näherung schrittweise nach folgender Vorschrift verbessert:64
wobei sich der Exponent 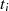 jeweils um
jeweils um 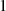 verringert (
verringert (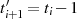 , mit
, mit 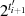 einem mglw. Vielfachen
der Ordnung
einem mglw. Vielfachen
der Ordnung 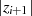 ).
).
Um die Verringerung des Exponenten nachzuweisen bilden wir einfach 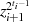 mit Hilfe von
Iterationsformel 4.28:
mit Hilfe von
Iterationsformel 4.28:
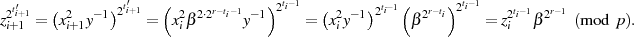
Beide Faktoren auf der rechten Seite sind aber vom Wert 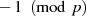 , was letztlich
, was letztlich
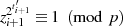
bedeutet. Zur Begründung folgende Argumentation:
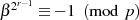 gilt wegen des EULER-Kriteriums für
gilt wegen des EULER-Kriteriums für 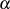 (siehe Kongruenz 4.27).
(siehe Kongruenz 4.27).
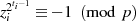 stützt sich auf die Darstellung:
stützt sich auf die Darstellung:
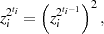
welche ja bei jeder Iteration als 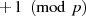 vorausgesetzt wird. Aus diesem Grund
kann der Wert innerhalb des Klammerausdrucks nur
vorausgesetzt wird. Aus diesem Grund
kann der Wert innerhalb des Klammerausdrucks nur 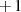 oder
oder 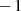 sein [NZM91,
Hilfssatz 2.10]. Wenn
sein [NZM91,
Hilfssatz 2.10]. Wenn 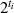 aber die Ordnung von
aber die Ordnung von 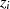 derstellt, dann muß
derstellt, dann muß 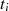 der kleinste
Wert sein, welcher zu
der kleinste
Wert sein, welcher zu 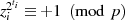 führt. Deshalb kann
führt. Deshalb kann 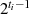 nicht (ebenfalls) die
Ordnung von
nicht (ebenfalls) die
Ordnung von 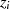 sein und es bleibt nur die Schlußfolgerung:
sein und es bleibt nur die Schlußfolgerung: 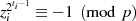 .
.
Aus dem letzten Punkt ergibt sich die Notwendigkeit, daß man am Anfang des Iterationszyklus
jedesmal die exakte Ordnung 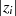 bzw. den zugehörigen Exponenten
bzw. den zugehörigen Exponenten 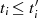 bestimmt (vgl. auch die
Erläuterungen zu den Startwerten).
bestimmt (vgl. auch die
Erläuterungen zu den Startwerten).
Algorithmus Bevor wir in Algorithmus 7 alle Erkenntnisse zusammenfassen, noch zwei Hinweise zur Umsetzung:
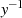 kann man einmalig zu Beginn des
Algorithmus durchführen.
kann man einmalig zu Beginn des
Algorithmus durchführen.
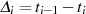 und führt in
Formel 4.28 die Abkürzungen
und führt in
Formel 4.28 die Abkürzungen

ein, dann kann man auch 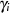 rekursiv berechnen:
rekursiv berechnen:
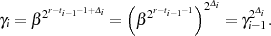
Um den korrekten Startwert 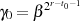 zu erzielen, vergleichen wir jetzt noch die Werte für
zu erzielen, vergleichen wir jetzt noch die Werte für
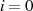 :
:
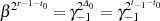
und erhalten:

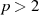 Ensure:
Ensure: 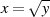
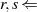 aus
aus 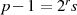 , mit
, mit  maximal
maximal
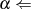 zufälliges Element aus
zufälliges Element aus 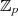
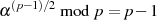 {EULER-Kriterium:
{EULER-Kriterium:
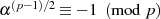 }
}
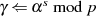 {
{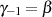 }
}
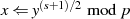 {
{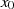 }
}
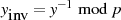
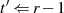
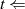 aus
aus 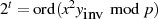 {Ordnung von
{Ordnung von
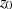 }
}
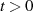 do
do
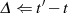
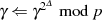 {
{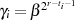 }
}
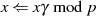
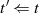
 aus
aus 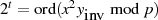 {Ordnung von
{Ordnung von
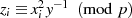 }
}
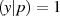 zu verifizieren}
zu verifizieren}
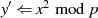
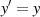 then
then