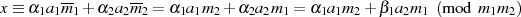Um sich dem Chinesischen Restsatz53
zu nähern, betrachten wir zunächst einen etwas einfacheren Fall, der die grundsätzliche
Fragestellung jedoch beinhaltet: Welche natürliche Zahl  erfüllt die folgenden beiden
Kongruenzen:
erfüllt die folgenden beiden
Kongruenzen:

wenn vorausgesetzt wird, daß 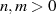 relativ prim zueinander sind?
relativ prim zueinander sind?
Um sie zu beantworten formulieren wir den Ausgangspunkt zuerst einmal entsprechend Restklassenbeziehung 3.2:
Deren Darstellung als
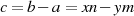 | (4.14) |
zeigt mit Verweis auf die Form von 4.10, daß es sich um eine lineare diophantische Gleichung handelt.
Wegen 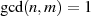 könnte die zugehörige Lösungsformel 4.12 zwar sofort zur Anwendung
kommen – naheliegend (da kurz) ist jedoch auch die Anwendung von BéZOUT’s Identität. Denn
multipliziert man
könnte die zugehörige Lösungsformel 4.12 zwar sofort zur Anwendung
kommen – naheliegend (da kurz) ist jedoch auch die Anwendung von BéZOUT’s Identität. Denn
multipliziert man 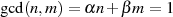 mit
mit  , dann kann aus
, dann kann aus
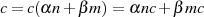
durch Vergleich mit 4.14 sofort abgelesen werden, daß 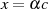 und
und 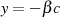 gelten
muß.54
Mit der Erkenntnis aus Formel 4.12, daß es sich bei den Lösungen einer linearen
diophantischen Gleichungen immer um eine ganze Lösungsmenge handelt,
resultiert:55
gelten
muß.54
Mit der Erkenntnis aus Formel 4.12, daß es sich bei den Lösungen einer linearen
diophantischen Gleichungen immer um eine ganze Lösungsmenge handelt,
resultiert:55

Durch Einsetzen in Formel 4.13 erhält man
und so eine geschlossene Darstellung für die Lösungsmenge.
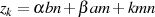 | (4.16) |
Mit der von den Restklassen bekannten Kongruenz 3.3 für teilerfremde Zahlen:56

können wir die Probe machen.

Die Lösungsmenge 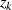 bildet demzufolge eine Restklasse
bildet demzufolge eine Restklasse ![[z]
mn](algebra1591x.png) .
.
Nehmen wir jetzt ein ganzes System von Kongruenzen an:
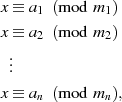
wobei 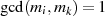 für
für 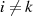 gelten soll. Wie schon im Fall von zwei Kongruenzen stellt
man die Frage, welche Lösung
gelten soll. Wie schon im Fall von zwei Kongruenzen stellt
man die Frage, welche Lösung  kongruent zu allen
kongruent zu allen 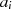 modulo
modulo 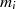 ist (
ist (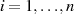 ).
Ohne einen exakten mathematischen Beweis anzutreten, scheint als Schlußfolgerung aus
Abschnitt 4.3.1 einleuchtend, daß die Lösung(en)
).
Ohne einen exakten mathematischen Beweis anzutreten, scheint als Schlußfolgerung aus
Abschnitt 4.3.1 einleuchtend, daß die Lösung(en)  eine Restklasse modulo
eine Restklasse modulo 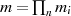 darstellen [Knu98, CP05].57
darstellen [Knu98, CP05].57
Bezeichnen wir mit 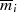 das Produkt aller Moduli ausgeschlossen
das Produkt aller Moduli ausgeschlossen 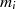 , also
, also
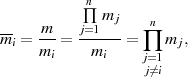
dann gilt wegen der Teilerfremdheit der einzelnen Moduli 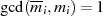 bzw. mit dem Satz von
BéZOUT:58
bzw. mit dem Satz von
BéZOUT:58
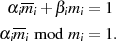
Im Gegensatz dazu verschwindet 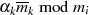 für
für 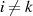 , denn
, denn 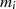 ist als Faktor in
ist als Faktor in 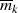 enthalten.
Die Orthogonalität beider Fälle kann mit Hilfe des KRONECKER-Symbols
enthalten.
Die Orthogonalität beider Fälle kann mit Hilfe des KRONECKER-Symbols 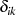 ausgedrückt
werden:
ausgedrückt
werden:
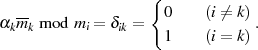
Die endgültige Lösungsidee besteht nun darin, für jede Kongruenz 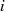 den folgenden Ausdruck zu
bilden:
den folgenden Ausdruck zu
bilden:
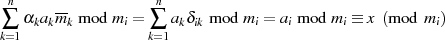
Wie zu sehen, ist die Summe auf der linken Seite kongruent zu 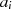 modulo
modulo 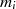 , was
, was
als finales Ergebnis rechtfertigt.
Für den einfachen Fall 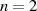 von Abschnitt 4.3.1 kann man mit
von Abschnitt 4.3.1 kann man mit 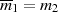 ,
, 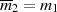 sowie
sowie

relativ einfach Kongruenz 4.17 verifizieren.59