


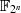
Quadratische Gleichungen (mit 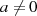 ) der Form
) der Form
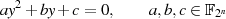
kann man bezüglich 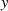 in
in 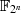 nicht so einfach lösen wie in
nicht so einfach lösen wie in 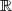 . Wie noch zu sehen sein wird, hat diese
Gleichung in
. Wie noch zu sehen sein wird, hat diese
Gleichung in 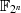 :
:
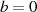 ;
;
Zuersteinmal kann man sie unter der Voraussetzung 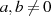 mit Hilfe der Substitution
mit Hilfe der Substitution 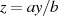 und
der naheliegenden Abkürzung
und
der naheliegenden Abkürzung 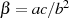 in eine allgemeine Form überführen:
in eine allgemeine Form überführen:
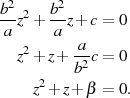
Davon ausgehend können wir uns den mathematischen Grundlagen einer Lösung zuwenden [Ber84, Sho05].
Zuallererst soll eine Hilfsformel eingeführt werden, welche in der einen oder anderen Form immer wieder
benötigt wird.65
Dazu sei die folgende Summe 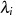 für ein Element
für ein Element 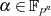 definiert und mit
definiert und mit 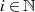 indiziert (vorerst
soll
indiziert (vorerst
soll 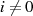 gelten):
gelten):
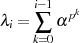
Dann berechnen wir unter Zuhilfenahme des „Anfänger-Traums“ nach Formel 3.13 bzw. 3.14 die
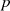 -te Potenz:
-te Potenz:
![[i−1 ]p i−1( ) i−1 i i−1
λp= αpk = αpk p = αpk+1 = αpk = αpi− α + αpk
i ∑k=0 k∑=0 k∑=0 k∑=1 ∑k=0](algebra1843x.png)
und stellen fest:
Definition
Der Trace ist die Summe der Konjugierten eines Elements im Körper 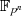 .
.
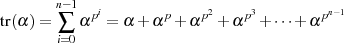
Mit Formel 4.29 ist der Trace auch darstellbar als:
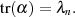 | (4.30) |
Eigenschaften
Mit Hilfe der Polynomdarstellung für ein Element 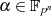
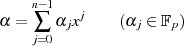
kann man einige interessante Eigenschaften und Beziehungen für den Trace ableiten:
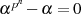 ) die Beziehungen:
) die Beziehungen:
d. h. der Trace ist eine lineare Abbildung 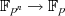 . Der Grund liegt ganz einfach darin, daß
Gleichung 4.31 nur im Körper
. Der Grund liegt ganz einfach darin, daß
Gleichung 4.31 nur im Körper 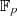 Gültigkeit hat (nicht in
Gültigkeit hat (nicht in 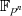 ) – und deshalb:
) – und deshalb:
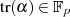 .
.
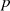 potenziert:
potenziert:
Warum dies so ist, erkennt man durch Anwendung der im Punkt 1 hergeleiteten Formel 4.31 sowie (wieder) des „Anfänger-Traums“ nach Formel 3.14:
![[ ]
n−1 ip n−1( i)p n− 1 pi
tr(α )= trp(α )= ∑ αp = ∑ αp = ∑ (αp ) = tr(αp).
i=0 i=0 i=0](algebra1858x.png)
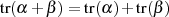 , mit
, mit 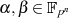
In ausführlicher Schreibweise des Trace und (wieder) mit Formel 3.14 kann man auch dies schnell beweisen.
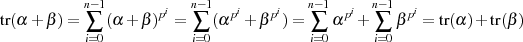
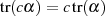 , mit
, mit 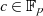 ,
, 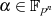
Ausklammern von 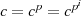 aus der Summendarstellung des Trace führt zu:
aus der Summendarstellung des Trace führt zu:
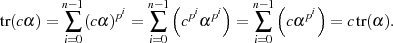
Im Körper 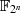 Speziell im Binärkörper
Speziell im Binärkörper 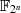 entsteht aus Formel 4.29:
entsteht aus Formel 4.29:
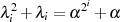 | (4.33) |
und mit der Rekursion 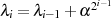 die (insbesondere für einen Berechnungsalgorithmus) interessante
Beziehung:66
die (insbesondere für einen Berechnungsalgorithmus) interessante
Beziehung:66
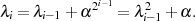 | (4.34) |
Insbesondere aus den Punkten 1 und 2 auf Seite 147 ergeben sich weitere spezialisierte Eigenschaften:
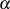 in
in 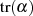 ändert nach Formel 4.32 nichts am Wert des
Trace.
ändert nach Formel 4.32 nichts am Wert des
Trace.
Grundlage des Beweises bilden die folgenden beiden Reduktionsfälle:
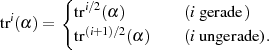
Sie erlauben es, den Exponenten iterativ bis auf 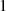 zu reduzieren, was letztlich zu
zu reduzieren, was letztlich zu
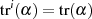 führt.
führt.
In einer kurzen Fallbetrachtung für 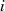 gerade:
gerade:
![i i∕2 2 i∕2
tr(α) = [tr (α)] = tr (α)](algebra1888x.png)
bzw. 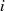 ungerade (und so
ungerade (und so  gerade):
gerade):
![tri(α )= tr(α )tri− 1(α )= tr(α )[tr(i− 1)∕2(α )]2 = tr(α)tr(i−1)∕2(α)= tr(i+1)∕2(α)](algebra1891x.png)
kann man die Begründung finden.
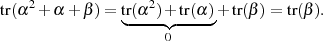
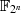 , ist die folgende:
, ist die folgende:
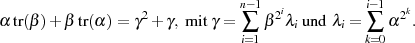 | (4.37) |
Ihr Beweis startet, indem man auf die äußere Summe den „Anfänger-Traum“ anwendet und
danach mit 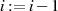 umindiziert. Mittels Formel 4.34 wird im Anschluß
umindiziert. Mittels Formel 4.34 wird im Anschluß 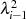 substituiert.
substituiert.
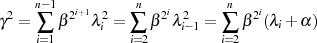
Läßt man die Summe bei  starten, dann ist zwar eine Korrektur um
starten, dann ist zwar eine Korrektur um 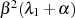 vonnöten,
letztlich ändert sich wegen
vonnöten,
letztlich ändert sich wegen 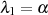 aber überhaupt nichts (
aber überhaupt nichts (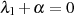 ). Jetzt noch den
Summanden für
). Jetzt noch den
Summanden für 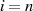 herausziehen, ausmultiplizieren und
herausziehen, ausmultiplizieren und 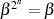 sowie
sowie 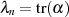 entsprechend Formel 4.30 berücksichtigen:
entsprechend Formel 4.30 berücksichtigen:
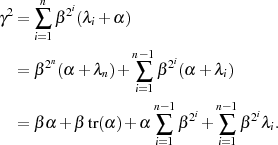
Im letzten Schritt wird noch der Summand für 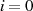 hinzugenommen:
hinzugenommen:
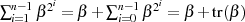 und man erkennt, daß der ganz rechte Term genau
und man erkennt, daß der ganz rechte Term genau 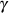 darstellt.
darstellt.
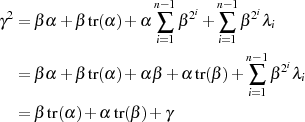
Algorithmus Die Idee für einen Algorithmus steckt in der Darstellung 4.30 für den Trace bzw. hinter Rekursionsformel 4.34.
Der Halb-Trace ist eine wichtige Funktion für den Fall, daß  für den Binärkörper
für den Binärkörper  ungerade
ist.
ungerade
ist.
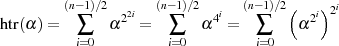
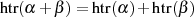
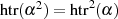 , es gilt jedoch hier:
, es gilt jedoch hier: 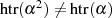 , wehalb
, wehalb 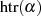 kein Element
aus
kein Element
aus 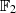 (im Gegensatz zum Trace), sondern aus
(im Gegensatz zum Trace), sondern aus  ist.
ist.
Einsetzen der Polynomdarstellung von 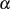 führt in ähnlicher Art und Weise wie beim
Trace zu:
führt in ähnlicher Art und Weise wie beim
Trace zu:
![[ ]2
2 (n− 1)∕2( 2)22i (n−1)∕2( 22i)2 (n−1)∕2 22i 2
htr(α )= ∑ α = ∑ α = ∑ α = htr(α )
i=0 i=0 i=0](algebra1927x.png)
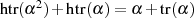
Etwas ausführlicher
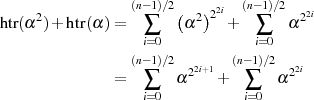
Umindizierung der beiden Summen mit 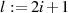 bzw.
bzw. 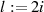 führt unter zusätzlicher
Berücksichtigung von
führt unter zusätzlicher
Berücksichtigung von 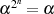 zum Ergebnis:
zum Ergebnis:
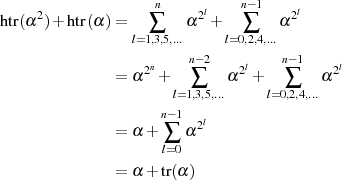
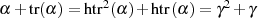 | (4.38) |
Algorithmus Der Algorithmus arbeitet ähnlich wie beim Trace (vgl. Algorithmus 8), außer daß der zusätzlichen Potenzierung Rechnung getragen wird.
Ist 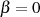 dann sind die Lösungen
dann sind die Lösungen 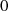 und
und 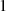 .
.
Im allgemeinen gilt:
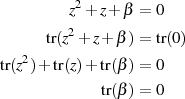
d. h. eine Voraussetzung für die Existenz der zwei Lösungen ist 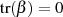 .
.
Für den Spezialfall, daß  ungerade ist, kann man mit der Grundvoraussetzung
ungerade ist, kann man mit der Grundvoraussetzung
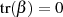 aus Formel 4.38 direkt eine Lösung der quadratischen Gleichung
ablesen:68
aus Formel 4.38 direkt eine Lösung der quadratischen Gleichung
ablesen:68
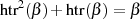 | (4.39) |
Mit ![htr2(β)+ htr(β)= [htr(β)+ 1]htr(β )](algebra1952x.png) sind die zwei Lösungen demzufolge
sind die zwei Lösungen demzufolge 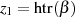 und
und
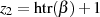 .
.
Ist  jedoch gerade (bzw. im allgemeinen Fall), dann besteht eine Berechnungsmöglichkeit durch
Anwendung von Formel 4.37. Setzt man nämlich als Grundvoraussetzung
jedoch gerade (bzw. im allgemeinen Fall), dann besteht eine Berechnungsmöglichkeit durch
Anwendung von Formel 4.37. Setzt man nämlich als Grundvoraussetzung 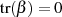 , dann
gilt:
, dann
gilt:
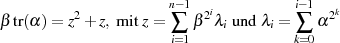
d. h. findet man ein Element 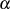 mit
mit 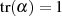 , wodurch
, wodurch
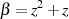
dann kann man die Lösung  aus diesem Element
aus diesem Element 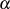 berechnen. Glücklicherweise besitzt im Mittel
die Hälfte aller Elemente
berechnen. Glücklicherweise besitzt im Mittel
die Hälfte aller Elemente 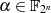 einen Trace von
einen Trace von 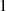 , so daß man
, so daß man 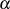 durchaus zufällig wählen kann
(mit 50% Wahrscheinlichkeit für
durchaus zufällig wählen kann
(mit 50% Wahrscheinlichkeit für 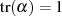 ).
).
Algorithmus
Für den allgemeinen Fall (bzw. wenn  gerade ist) kann man auf Algorithmus 10 zurückgreifen, um
die quadratische Gleichung in
gerade ist) kann man auf Algorithmus 10 zurückgreifen, um
die quadratische Gleichung in 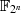 zu lösen [ANS05, IEE00].
zu lösen [ANS05, IEE00].
Beide Summen können vereint werden, wenn man 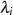 iterativ in der äußeren Summe mitberechnet
(nach derselben Methodik wie in Algorithmus 8), was dann im letzten Durchlauf
iterativ in der äußeren Summe mitberechnet
(nach derselben Methodik wie in Algorithmus 8), was dann im letzten Durchlauf 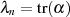 ergibt.
ergibt.
Und es gilt ja nach Formel 4.37, unter der Voraussetzung 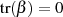 und
und 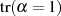 , immer:
, immer:
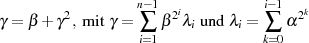
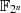
Optimierung
Schreibt man dazu unter Zuhilfenahme der Polynomdarstellung für das Element 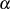 und noch unter
Berücksichtigung von Formel 3.13:
und noch unter
Berücksichtigung von Formel 3.13:
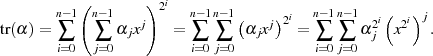
Umsortieren der Summen und mit 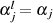 in
in 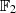 und dann wieder mit Formel 3.13
und dann wieder mit Formel 3.13
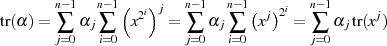
Den Wert für 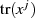 kann man vorausberechnen.
kann man vorausberechnen.