


Gleichungen mit ausschließlich ganzzahligen Lösungen  nennt man diophantisch, wobei
sie im linearen Fall (für zwei Variablen) die folgende Form haben:
nennt man diophantisch, wobei
sie im linearen Fall (für zwei Variablen) die folgende Form haben:
 | (4.10) |
Solche Gleichungen haben genau dann eine Lösung, wenn der größte gemeinsame Teiler
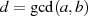 den Wert
den Wert  teilt. Im Zusammenhang mit EUKLID’s Algorithmus wurde dies praktisch
schon nachgewiesen – auch daß es unendlich viele solcher Lösungen gibt, kam in Abschnitt 4.1.1 zur
Sprache.
teilt. Im Zusammenhang mit EUKLID’s Algorithmus wurde dies praktisch
schon nachgewiesen – auch daß es unendlich viele solcher Lösungen gibt, kam in Abschnitt 4.1.1 zur
Sprache.
Zuerst bemerken wir, daß die Differenz zweier Lösungen 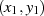 und
und 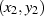 die homogene
Gleichung
die homogene
Gleichung 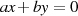 erfüllt.
erfüllt.
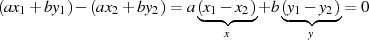
Mit 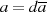 und
und 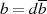 läßt sich sogar schreiben
läßt sich sogar schreiben
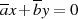
und es liegen die Lösungen 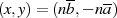 ,
, 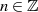 auf der Hand (Einsetzen ergibt
auf der Hand (Einsetzen ergibt
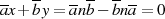 ).52
Findet man jetzt noch eine partikuläre Lösung
).52
Findet man jetzt noch eine partikuläre Lösung 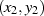 , dann ergeben sich alle weiteren
zu:
, dann ergeben sich alle weiteren
zu:

Partikuläre Lösungen 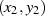 für
für 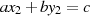 haben wir aber schon mittels der erweiterten
GCD-Algorithmen zur Verfügung, denn mit der BéZOUT’s Identität (den Index
haben wir aber schon mittels der erweiterten
GCD-Algorithmen zur Verfügung, denn mit der BéZOUT’s Identität (den Index 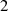 jetzt
weggelassen)
jetzt
weggelassen)
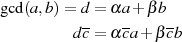
gilt:
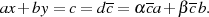
Eine partikuläre Lösung (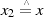 ,
, 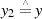 ) kann deshalb mit Hilfe der BéZOUT-Kofaktoren
) kann deshalb mit Hilfe der BéZOUT-Kofaktoren 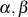 gegeben werden.
gegeben werden.

Die Vielfalt aller Lösungen stellt sich dadurch wiefolgt dar:
Für den Spezialfall 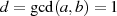 entartet die Formel zu:
entartet die Formel zu: