Definition

3.1 Definition

Restklassen sind Kongruenzen von Elementen (einer algebraischen Struktur) modulo eines fixen Elements $m$ . Das Rechnen mit solchen Elementen wird als modulare oder Modulo-Arithmetik und $m$ als das Modul bezeichnet. In diesem Sinne definiert man

r ≡ a mod m

(3.1)

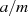als den Rest $r$ , der bei der „Division“ $a∕m$ entsteht und sagt: $r$ ist kongruent $a$ modulo $m$ . Im Umkehrschluß sind die Restklassenelemente durch die Relation

a = qm + r, 0 ≤ r < m

(3.2)

bestimmt. Die Äquivalenzrelation 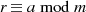$r ≡ a mod m$ kann man z. B. im Ring der ganzen Zahlen 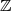$ℤ$ definieren, ist aber nicht auf diesen beschränkt. Im allgemeinen Fall 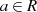$a ∈ R$ schreibt man für die Restklasse

[r]m = {a|a ∈R, r ≡ a mod m},

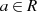d. h. die Restklasse $[r]m$ ist die Menge aller Elemente $a∈ R$ , die bei der Division modulo $m$ genau den Rest $r$ ergeben. Ein Beispiel für 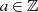$a∈ ℤ$ mit einem Modul von 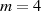$m = 4$ soll das veranschaulichen.

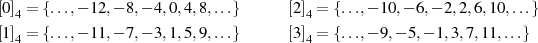
Üblicherweise bezeichnet man die Menge aller Restklassen mit

Rm = {[r0]m,[r1]m,...,[rn− 1]m},

also z. B. für die ganzen Zahlen 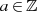$a ∈ℤ$ modulo $m$ :

ℤ = ℤ∕mℤ = {[0] ,[1] ,...,[m− 1] }. m m m m

Im Allgemeinen werden Verknüpfungsoperationen (Addition, Multiplikation usw.) zwischen zwei Restklassen dadurch definiert, daß man jeweils einen Vertreter aus den Restklassen auswählt und dann die Operation mit diesem Repräsentanten durchführt.