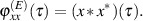Nehmen wir nun an, wir betrachten eine Realisierung 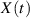 zu zwei Zeitpunkten
zu zwei Zeitpunkten 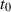 und
und 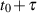 .
Obwohl für stationäre Zufallsprozesse der Zeitpunkt
.
Obwohl für stationäre Zufallsprozesse der Zeitpunkt 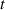 keine Rolle spielt, wird trotzdem (zumindest
unter dem Blickwinkel der Allgemeinheit) eine stochastische Abhängigkeitsbeziehung zwischen
keine Rolle spielt, wird trotzdem (zumindest
unter dem Blickwinkel der Allgemeinheit) eine stochastische Abhängigkeitsbeziehung zwischen
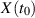 und
und 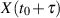 bestehen. Bezeichnen wir nun zwei Zufallsvariablen mit
bestehen. Bezeichnen wir nun zwei Zufallsvariablen mit 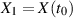 und
und 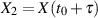 und stellen die Frage nach einer der wesentlichsten Eigenschaften des
Zufallsvektors
und stellen die Frage nach einer der wesentlichsten Eigenschaften des
Zufallsvektors 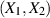 – nämlich der Abhängigkeit (bzw. Unabhängigkeit) von
– nämlich der Abhängigkeit (bzw. Unabhängigkeit) von 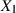 und
und
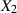 . Dazu haben wir schon geeignete Maße kennengelernt, nämlich die Kovarianz und den
Korrelationskoeffizienten. Um ausgehend von deren Definition jedoch fortfahren zu können, müssen
wir noch Existenz und Kenntnis der verbundenen Wahrscheinlichkeitsdichte des zweidimensionalen
Vektors
. Dazu haben wir schon geeignete Maße kennengelernt, nämlich die Kovarianz und den
Korrelationskoeffizienten. Um ausgehend von deren Definition jedoch fortfahren zu können, müssen
wir noch Existenz und Kenntnis der verbundenen Wahrscheinlichkeitsdichte des zweidimensionalen
Vektors 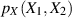 voraussetzen. Nun definieren wir eine neue (aber dennoch mit
voraussetzen. Nun definieren wir eine neue (aber dennoch mit 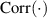 und
und 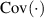 eng verwandte) Größe und bezeichnen sie als Korrelation
eng verwandte) Größe und bezeichnen sie als Korrelation 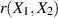 zweier
Zufallsgrößen:26
zweier
Zufallsgrößen:26
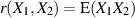
Gleichbedeutend ist auch der folgende Ausdruck, wenn man Formel 24 berücksichtigt.
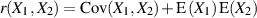
Erinnern wir uns an den Ausgangspunkt und ersetzen die (zur besseren Anschauung eingeführten)
Zufallsgrößen 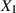 und
und 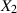 wieder durch die Realisierung
wieder durch die Realisierung 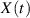 .
.
![r[X(t ),X (t + τ)]= E [X (t )X(t +τ )]
0 0 0 0](probabil466x.png)
Ferner berücksichtigen wir, daß für stationäre Zufallsprozesse der Zeitpunkt 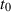 keine Bedeutung hat –
und definieren die sogenannte Autokorrelationsfunktion von
keine Bedeutung hat –
und definieren die sogenannte Autokorrelationsfunktion von 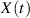 .
.
![E(X)=0
φxx(τ) = E[X(t)X(t+ τ)] = Cov [X (t),X (t+ τ)]](probabil469x.png)
Für eine kontinuierliche Realisierung 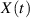 des Zufallsprozesses
des Zufallsprozesses 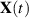 berechnet sich dieser
Erwartungswert wiefolgt (vgl. Abschnitt 3.4):
berechnet sich dieser
Erwartungswert wiefolgt (vgl. Abschnitt 3.4):
![∫ ∞ ∫ ∞
φxx(τ)= x(t)x(t+ τ)pX [x(t)x(t+ τ)]dx(t)dx(t+ τ).
−∞ −∞](probabil472x.png)
Für ergodische Prozesse nimmt man nun zusätzlich noch an, daß der Erwartungswert ![E[X(t)X(t+ τ)]](probabil473x.png) aus der Zeitfunktion
aus der Zeitfunktion 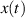 als (Selbst-) Ähnlichkeitsmaß folgendermaßen bestimmt werden
kann.
als (Selbst-) Ähnlichkeitsmaß folgendermaßen bestimmt werden
kann.
![1 ∫ ----------
φxx(τ)= E [x(t)x(t+ τ)]= lim -- x(t)x(t+ τ)dt = x(t)x(t+ τ)
T→ ∞T T](probabil475x.png) | (52) |
Die dadurch definierte Autokorrelationsfunktion (AKF) hat folgende Eigenschaften:
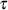 eine gerade Funktion, d. h.
eine gerade Funktion, d. h. 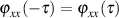 .
.
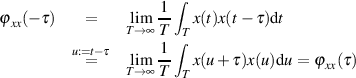
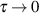 ist ist sie gleich dem Quadrat des Effektivwertes (bzw. der mittleren Leistung
ist ist sie gleich dem Quadrat des Effektivwertes (bzw. der mittleren Leistung 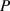 des
Signals), vorausgesetzt
des
Signals), vorausgesetzt 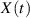 ist keine aperiodische oder determinierte Funktion, sondern ein
echter Zufallsprozeß.
ist keine aperiodische oder determinierte Funktion, sondern ein
echter Zufallsprozeß.
![1∫ 2 [ 2 ] 2
φxx(0)= Tli→m∞T- T x(t)dt = E X (t) = X~ = P](probabil482x.png) | (53) |
In der Umgebung von 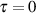 ist insbesondere der Abfall von
ist insbesondere der Abfall von 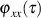 ein Maß für die
Regellosigkeit des Prozesses.
ein Maß für die
Regellosigkeit des Prozesses.
Ist 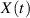 aber ein determiniertes Energiesignal (charakterisiert durch
aber ein determiniertes Energiesignal (charakterisiert durch 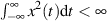 ), dann
wird üblicherweise die Definition der AKF (sowie aller daraus abgeleiteten Größen) geringfügig
modifiziert.27
), dann
wird üblicherweise die Definition der AKF (sowie aller daraus abgeleiteten Größen) geringfügig
modifiziert.27
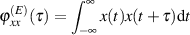 | (54) |
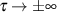 kann man annehmen, daß
kann man annehmen, daß 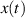 und
und 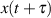 vollständig unabhängig sind,
weshalb dann
vollständig unabhängig sind,
weshalb dann
![∫ ∫ [ ∫ ]2 ----
lim φ (τ)= lim 1- x(t)dt x(t)dt = lim 1- x(t)dt = x(t)2
τ→± ∞ xx T→ ∞T T T T→∞ T T](probabil493x.png)
gilt. Hat der Zufallsprozeß keine systematischen (oder determinierte) Anteile und außerdem
einen zeitlichen Mittelwert 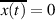 , dann verschwindet die Autokorrelationsfunktion im
Unendlichen:
, dann verschwindet die Autokorrelationsfunktion im
Unendlichen: 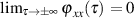 .
.
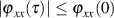 .28
.28
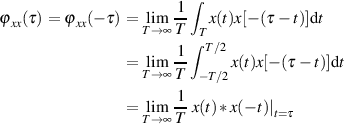
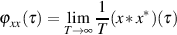 | (55) |
Für (determinierte) Energiesignale entfällt der Limes, d. h. die “Energie-AKF” ist ganz einfach die Faltung