


Eine Gruppe2
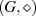 ist ein algebraisches System, daß aus einer nicht-leeren Menge von Elementen
ist ein algebraisches System, daß aus einer nicht-leeren Menge von Elementen 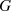 besteht,
für die eine Operation
besteht,
für die eine Operation  mit folgenden Eigenschaften definiert ist [PW72, 2.1], [Kör88,
101 ff.]:
mit folgenden Eigenschaften definiert ist [PW72, 2.1], [Kör88,
101 ff.]:
 auf zwei Elemente muß wieder zu einem Element in
auf zwei Elemente muß wieder zu einem Element in 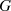 führen (Abgeschlossenheit):
führen (Abgeschlossenheit): 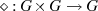 ;
;
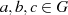 muß gelten:
muß gelten: 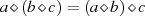 (Assoziativität);
(Assoziativität);
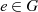 muß existieren, so daß gilt:
muß existieren, so daß gilt: 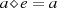 mit
mit 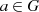 (Identität);
(Identität);
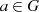 muß ein inverses Element
muß ein inverses Element 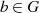 existieren, so daß
existieren, so daß 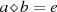 gilt.
gilt.Die Menge 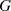 kann aus einer endlichen oder unendlichen Anzahl von Elementen
kann aus einer endlichen oder unendlichen Anzahl von Elementen 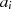 bestehen. Bei
einer Aufzählung der Elemente werden diese in geschweifte Klammern eingeschlossen, z. B. so:
bestehen. Bei
einer Aufzählung der Elemente werden diese in geschweifte Klammern eingeschlossen, z. B. so:
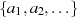 . Ist die Zusatzbedingung
. Ist die Zusatzbedingung 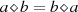 erfüllt, wird die Gruppe kommutativ bzw.
ABEL’sch genannt.
erfüllt, wird die Gruppe kommutativ bzw.
ABEL’sch genannt.
Die Ordnung (auch Mächtigkeit oder Kardinalität) einer Gruppe ist die Anzahl der Elemente in
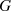 , geschrieben als
, geschrieben als 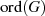 ,
, 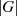 oder auch
oder auch  . Ist
. Ist 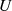 eine Teilmenge von
eine Teilmenge von 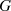 , d. h.
, d. h.
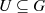 , dann wird
, dann wird 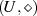 als Untergruppe von
als Untergruppe von 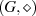 bezeichnet, wenn mit derselben
Operation
bezeichnet, wenn mit derselben
Operation  auch
auch 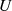 alle Eigenschaften einer Gruppe erfüllt [Bos96, 1.], [PW72, 2.4]. Der
Zusammenhang zwischen der Ordnung von
alle Eigenschaften einer Gruppe erfüllt [Bos96, 1.], [PW72, 2.4]. Der
Zusammenhang zwischen der Ordnung von 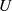 und der von
und der von 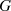 wird durch den Satz von LAGRANGE
beschrieben.
wird durch den Satz von LAGRANGE
beschrieben.
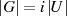 | (1.1) |
Die Ordnung 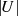 ist danach ein Teiler von
ist danach ein Teiler von 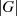 und
und 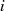 der so genannte Index von
der so genannte Index von
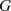 über
über 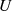 (bzw. Index von
(bzw. Index von 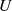 in
in 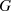 ), welcher auch als
), welcher auch als 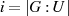 geschrieben
wird.3
geschrieben
wird.3
Entsprechend der allgemeinen Definition wird eine Menge 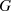 additive Gruppe
additive Gruppe 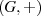 genannt, wenn
für sie
genannt, wenn
für sie
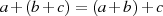 mit
mit 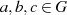 definiert ist;
definiert ist;
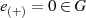 mit der Beziehung
mit der Beziehung 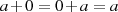 für alle
für alle
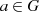 existiert;
existiert;
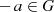 zu
zu 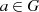 mit der Relation
mit der Relation
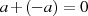 definiert ist.
definiert ist.Das bekannteste Beispiel einer solchen Gruppe ist die der ganzen Zahlen 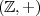 .
.
Für die multiplikative Gruppe 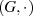 gilt äquivalent:
gilt äquivalent:
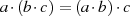 mit
mit 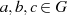 ;
;
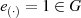 mit der Identität
mit der Identität 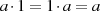 für
für 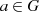 ;
;
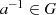 zu jedem
zu jedem 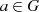 mit der Relation
mit der Relation 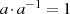
sind definiert. Zur Multiplikation ist zu bemerken, daß nicht-negative Potenzen eines Elements induktiv definiert sind

also durch  -malige Multiplikation.
-malige Multiplikation.
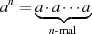
Das Nullelement 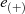 einer additiven Gruppe kann in einer multiplikativen Gruppe nicht
enthalten sein, denn es ist grundsätzlich nicht invertierbar (siehe auch Abschnitt 1.3 zu den
Körpern).
einer additiven Gruppe kann in einer multiplikativen Gruppe nicht
enthalten sein, denn es ist grundsätzlich nicht invertierbar (siehe auch Abschnitt 1.3 zu den
Körpern).