


Bei der Methode nach MONTGOMERY handelt es sich eigentlich um eine Multiplikationsmethode, bei der die Modulo-Reduktion des (Zwischen-) Ergebnisses ohne echte Langzahldivision erfolgen kann [Mon85], [CP05, 9.2.1], [HMV04, 2.2.4]. Da allerdings zuerst eine Transformation beider Faktoren in den MONTGOMERY-“Raum“ vorgenommen werden muß (welche zwei Modulo-Division erfordert) und außerdem einmal der erweiterte GCD-Algorithmus bemüht werden muß, kommen die Geschwindigkeitsvorteile nur bei der Potenzierung wirklich zum tragen.
Um einen leicht verständlichen Zugang zu finden, konzentrieren wir uns auf eine einzelne Multiplikation
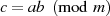 . Dazu soll eine Zahl
. Dazu soll eine Zahl  vorausgesetzt werden, die keinen gemeinsamen Teiler mit
dem Modul
vorausgesetzt werden, die keinen gemeinsamen Teiler mit
dem Modul  hat und für die
hat und für die  gewährleistet ist. Die MONTGOMERY-Multiplikation kann man
nun, unter der Voraussetzung
gewährleistet ist. Die MONTGOMERY-Multiplikation kann man
nun, unter der Voraussetzung 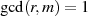 (bzw. mit dem Satz von BéZOUT
(bzw. mit dem Satz von BéZOUT 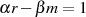 ), in
folgenden Einzelschritten darstellen:
), in
folgenden Einzelschritten darstellen:
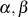 mit Hilfe des erweiterten euklidischen
Algorithmus;
mit Hilfe des erweiterten euklidischen
Algorithmus;
 und
und 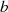 zu
zu 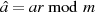 und
und 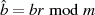 (eine normale Modulo-Division);
(eine normale Modulo-Division);
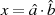 (man beachte, daß hierbei keine
Modulo-Reduktion vorgenommen wird);
(man beachte, daß hierbei keine
Modulo-Reduktion vorgenommen wird);
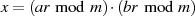 zu
zu
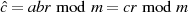 ;
;
Die nötige Korrektur69
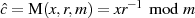 führt zu einer MONTGOMERY-Darstellung für
führt zu einer MONTGOMERY-Darstellung für  (als
Voraussetzung für den nächsten Teilschritt).70
(als
Voraussetzung für den nächsten Teilschritt).70
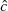 als
einen der Faktoren verwendet;
als
einen der Faktoren verwendet;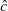 zu
zu 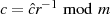 , ebenfalls eine
MONTGOMERY-Reduktion:
, ebenfalls eine
MONTGOMERY-Reduktion: 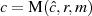 .
.MONTGOMERY-Reduktion
Zur Herleitung von MONTGOMERY’s effizienter Berechnungsmethode für 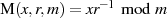 wählen wir als Ausgangspunkt:
wählen wir als Ausgangspunkt:
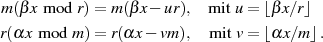
Subtraktion beider Gleichungen ergibt
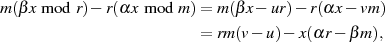
was mit 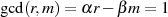 zu
zu
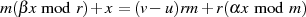
führt.71
Mit dem Wissen, daß es sich bei 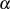 um das multiplikativ inverse Element von
um das multiplikativ inverse Element von  im Restklassensystem
modulo
im Restklassensystem
modulo  handelt (
handelt (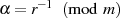 ,
, 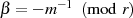 ), stellen wir noch um:
), stellen wir noch um:
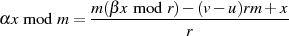
und gewinnen letztlich MONTGOMERY’s Reduktionsformel.
Praktisch benötigt man  und
und  nicht, sondern geht meist nach folgendem Algorithmus
vor:
nicht, sondern geht meist nach folgendem Algorithmus
vor:
Bei geschickter Wahl von  zum Beispiel als
zum Beispiel als 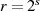 sind für alle
(Modulo-) Divisionen in Formel 4.40 nur logische oder Schiebeoperationen
nötig.72
Um
sind für alle
(Modulo-) Divisionen in Formel 4.40 nur logische oder Schiebeoperationen
nötig.72
Um 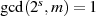 zu garantieren ist die einfachste Bedingung die,
zu garantieren ist die einfachste Bedingung die,  als ungerade
vorauszusetzen.73
als ungerade
vorauszusetzen.73