


Der TSCHEBYSCHEff-Tiefpaß vom Typ II ist ebenfalls eine Anwendung der TSCHEBYSCHEff-Funktionen
erster Art – diesmal aber so, daß eine Welligkeit im Durchlaßbereich vermieden wird, dafür aber
Dämpfungsminima im Sperrbereich hingenommen werden müssen [Fri79a, 2.2.1.1]. Aus
mathematischer Sicht handelt es sich um eine Bestapproximation der “Konstanten” Unendlich für alle
Frequenzen größer als die Sperrfrequenz 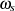 (siehe auch Abschnitt 2.1.2). Äquivalent dazu kann man
die Forderung formulieren, daß
(siehe auch Abschnitt 2.1.2). Äquivalent dazu kann man
die Forderung formulieren, daß 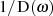 im Sperrbereich die Nullinie bestmöglich nähern
möge.16
Weil das (Best-) Approximationsintervall der TSCHEBYSCHEff-Funktionen im vorgenannten
Sinne aber
im Sperrbereich die Nullinie bestmöglich nähern
möge.16
Weil das (Best-) Approximationsintervall der TSCHEBYSCHEff-Funktionen im vorgenannten
Sinne aber ![[− 1,+1 ]](stdfilter573x.png) ist, muß eine entsprechende Abbildung auf den Sperrbereich
erfolgen.17
Aus diesen logischen Überlegungen heraus kann man die Drosselungsfunktion für den inversen
TSCHEBYSCHEff-Tiefpaß ableiten.
ist, muß eine entsprechende Abbildung auf den Sperrbereich
erfolgen.17
Aus diesen logischen Überlegungen heraus kann man die Drosselungsfunktion für den inversen
TSCHEBYSCHEff-Tiefpaß ableiten.
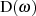 sich auf der Grundlage von Formel 2.1 in einem typischen Dämpfungsverlauf darstellt
zeigt Abbildung 2.6. Die maximale Dämpfung im Durchlaßbereich liegt an der normierten
Grenzfrequenz
sich auf der Grundlage von Formel 2.1 in einem typischen Dämpfungsverlauf darstellt
zeigt Abbildung 2.6. Die maximale Dämpfung im Durchlaßbereich liegt an der normierten
Grenzfrequenz 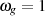 und hat den Wert:
und hat den Wert:
![[ 2 ] ( 2)
Amax = 10 log 1 + D (1) = 10log 1 +σ .](stdfilter578x.png)
Die minimale Dämpfung im Sperrbereich (inklusive 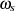 ) wird durch die Funktionswerte
) wird durch die Funktionswerte 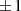 an den
Extremstellen von
an den
Extremstellen von 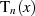 bestimmt (vgl. Anhang ??).
bestimmt (vgl. Anhang ??).
![[ ] [ ] [ ]
Amin = 10log 1+ D2(ωs) = 10log 1+ σ2T2n(ωs) = 10log 1+ σ 2cosh2(narcoshωs)](stdfilter582x.png)
Die zugehörigen  -Werte liegen bei
-Werte liegen bei 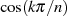 , also bezüglich
, also bezüglich 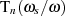 an den Stellen
an den Stellen
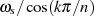 . Die immer dazwischen liegenden Dämpfungsmaxima werden durch die Nullstellen
der TSCHEBYSCHEff-Funktion erzeugt und sind deshalb bei
. Die immer dazwischen liegenden Dämpfungsmaxima werden durch die Nullstellen
der TSCHEBYSCHEff-Funktion erzeugt und sind deshalb bei ![ωs∕cos[(k− 1∕2 )π ∕n]](stdfilter587x.png) lokalisiert.
Kombiniert man (wie beim TSCHEBYSCHEff-Tiefpaß vom Typ I) auch hier beide Ausdrücke, so
erhält man die Frequenzen
lokalisiert.
Kombiniert man (wie beim TSCHEBYSCHEff-Tiefpaß vom Typ I) auch hier beide Ausdrücke, so
erhält man die Frequenzen 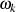 nach Abbildung 2.6.
nach Abbildung 2.6.

Aufgrund der für 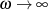 geltenden Tatsache
geltenden Tatsache
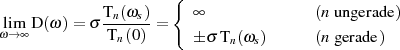
werden praktisch meist Tiefpässe mit ungeradem Grad bevorzugt.
Im Gegensatz zum ersten Typ des TSCHEBYSCHEff-Tiefpaß besitzt 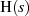 hier Nullstellen, die wegen
der Dämpfungsextrema im Sperrbereich sogar auf der
hier Nullstellen, die wegen
der Dämpfungsextrema im Sperrbereich sogar auf der 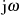 -Achse liegen müssen. Um sie zu bestimmen
bilden wir (wie üblich) zuerst das Betragsquadrat der Übertragungsfunktion
-Achse liegen müssen. Um sie zu bestimmen
bilden wir (wie üblich) zuerst das Betragsquadrat der Übertragungsfunktion  , gehen dann in den
LAPLACE-Bildbereich über
, gehen dann in den
LAPLACE-Bildbereich über
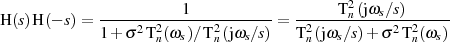 | (2.22) |
und setzen den Zähler Null.
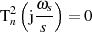
Von der Betrachtung der Extremwerte her (vgl. voriger Abschnitt oder Anhang ??) ist schon bekannt,
daß die Nullstellen von 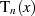 bei
bei
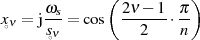
liegen und deshalb bezüglich  bei
bei
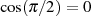 die Nullstelle für
die Nullstelle für 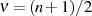 im Unendlichen zum Liegen kommt. Aus
diesem Grund kann sie nicht als solche angesehen werden, sondern eher als Hinweis,
daß der Grad des Zählerpolynoms von
im Unendlichen zum Liegen kommt. Aus
diesem Grund kann sie nicht als solche angesehen werden, sondern eher als Hinweis,
daß der Grad des Zählerpolynoms von 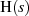 größer als der des Nennerpolynoms
ist.18
größer als der des Nennerpolynoms
ist.18
Zur Ermittlung der Pole von 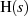 kann man entweder formal die Polstellenbedingung für
Gleichung 2.22 formulieren oder (was dasselbe ist) den höheren Zusammenhang zwischen Drosselung
und Übertragungsfunktion nach Formel 2.1 berücksichtigen. Wählt man letzteren Ansatz, dann ist
sofort erkennbar, daß alle Pole durch die Beziehung
kann man entweder formal die Polstellenbedingung für
Gleichung 2.22 formulieren oder (was dasselbe ist) den höheren Zusammenhang zwischen Drosselung
und Übertragungsfunktion nach Formel 2.1 berücksichtigen. Wählt man letzteren Ansatz, dann ist
sofort erkennbar, daß alle Pole durch die Beziehung 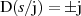 charakterisiert sind. Nehmen wir
also die Drosselungsfunktion dieses Filtertyps nach Gleichung 2.21 und formulieren als
Bedingung:
charakterisiert sind. Nehmen wir
also die Drosselungsfunktion dieses Filtertyps nach Gleichung 2.21 und formulieren als
Bedingung:
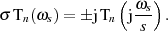
Wegen der Ähnlichkeit mit Gleichung 2.18 des Typ I Tiefpaß substituieren wir 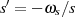 und
und
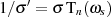 und erhalten:
und erhalten:
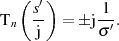
Nun steht einer Wiederverwendung der in Abschnitt 2.3.2 gewonnenen Lösung
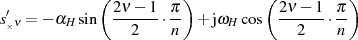 | (2.24) |
nichts mehr im Wege. Wir ersetzen nur noch die Zwischenvariablen (mit Strich) und erhalten für die Pole:19
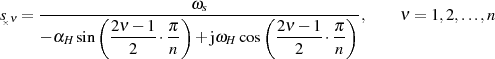
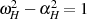 ) der elliptischen Verteilung: Man verifiziert an Hand der Formeln, daß die Lage der Polstellen qualitativ dieselbe wie beim ersten
Typ des TSCHEBYSCHEff-Tiefpaß (siehe Abbildung 2.5) ist.
) der elliptischen Verteilung: Man verifiziert an Hand der Formeln, daß die Lage der Polstellen qualitativ dieselbe wie beim ersten
Typ des TSCHEBYSCHEff-Tiefpaß (siehe Abbildung 2.5) ist.