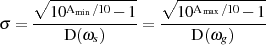Bei der Annäherung einer Zielfunktion im Frequenzbereich sind im allgemeinen zwei systemtheoretische
Größen interessant: die Dämpfung 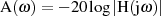 sowie der Phasengang
sowie der Phasengang  .
Fast alle Standard-Tiefpässe beschränken sich dabei auf die gleichmäßige (TSCHEBYSCHEff-)
Approximation des Amplitudenganges
.
Fast alle Standard-Tiefpässe beschränken sich dabei auf die gleichmäßige (TSCHEBYSCHEff-)
Approximation des Amplitudenganges 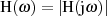 , vgl. [Gui52, Gui57, Win54, Zve67, Fri79a,
Mil92].1
Dazu wird üblicherweise statt der Amplitudencharakteristik
, vgl. [Gui52, Gui57, Win54, Zve67, Fri79a,
Mil92].1
Dazu wird üblicherweise statt der Amplitudencharakteristik 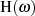 die charakteristische Funktion
die charakteristische Funktion
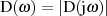 , welche auch Drosselung genannt wird, herangezogen. Als Zusammenhang zwischen
beiden Größen gilt bekanntlich:
, welche auch Drosselung genannt wird, herangezogen. Als Zusammenhang zwischen
beiden Größen gilt bekanntlich:
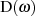 viel schwächer, d. h.
fast jede rationale Funktion ist hier erlaubt [Zve67, 2.15].2
viel schwächer, d. h.
fast jede rationale Funktion ist hier erlaubt [Zve67, 2.15].2
Für die Verwendung bekannter mathematischer Lösungsfunktionen der gleichmäßigen Approximation
(bezeichnet mit 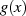 ) macht es sich außerdem günstig, die Drosselung als Produkt von
) macht es sich außerdem günstig, die Drosselung als Produkt von 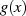 mit einer
Konstanten
mit einer
Konstanten 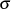 zu definieren.
zu definieren.
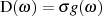 | (2.2) |
In Tabelle 2.1 sind nun ausgewählte Approximationsintervalle bzw. -punkte sowie die Zusammenhänge mit den soeben eingeführten Größen dargelegt.
| Tabelle 2.1: | Approximationskenngrößen |
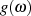 | 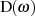 | 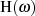 | 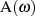 |
|
| Durchlaßbereich | 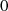 | 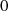 |  |  |
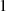 |  | 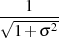 | 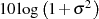 |
|
| Sperrbereich |  |  |  |  |
Die Definition von Durchlaß- und Sperrbereich beruht auf dem Fakt, daß (fast)
alle konventionellen Standard-Filter den idealen Tiefpaß (zumindest stückweise)
approximieren. Es wird deshalb für den Durchlaßbereich das Intervall 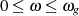 angenommen,3
für den Sperrbereich
angenommen,3
für den Sperrbereich 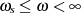 . Man erhält damit ein Tiefpaß-Toleranzschema nach Abbildung 2.1, das
außerdem eine maximale (erlaubte) Durchlaß-Dämpfung
. Man erhält damit ein Tiefpaß-Toleranzschema nach Abbildung 2.1, das
außerdem eine maximale (erlaubte) Durchlaß-Dämpfung 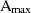 und eine minimale Sperr-Dämpfung
und eine minimale Sperr-Dämpfung 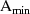 definiert.4
definiert.4
Im Zusammenhang mit der Approximationsfunktion soll noch kurz angemerkt sein, daß die Extremstellen der Dämpfung sich auf der Grundlage von
![A (ω )= − 20log|H(jω)|= 10log[1 + D2(ω)]= 10log [1+ σ2g2(ω)]](stdfilter383x.png)
aus den Nullstellen von 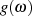 als auch deren Ableitung
als auch deren Ableitung 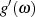 zusammensetzen.
zusammensetzen.
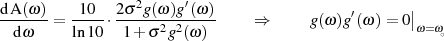
P. L. TSCHEBYSCHEff hat im 19. Jahrhundert mit dem nach ihm benannten Alternantensatz die grundlegende Bedingung für eine Bestapproximation gefunden [Tsc07, Mei64, Kör88]. In kurzer Form ist der Inhalt folgender:
Eine Bestapproximation5
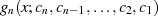 der Funktion
der Funktion 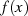 im Intervall
im Intervall ![[a,b]](stdfilter392x.png) durch eine Funktion
geringster Abweichung
durch eine Funktion
geringster Abweichung 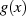 , d. h. eine Näherung für die folgende TSCHEBYSCHEff-Norm
gilt:
, d. h. eine Näherung für die folgende TSCHEBYSCHEff-Norm
gilt:
ist dadurch gekennzeichnet, daß die Fehlerfunktion 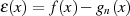 an
an  verschiedenen Punkten
verschiedenen Punkten 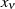
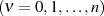 alternierend den Wert
alternierend den Wert 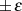 annimmt.
Dabei muß der Punkt
annimmt.
Dabei muß der Punkt 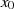 genau auf den Intervallanfang
genau auf den Intervallanfang  und
und 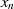 auf den
Endpunkt
auf den
Endpunkt 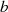 fallen.
fallen.
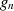 geringster Abweichung meist die Drosselung
geringster Abweichung meist die Drosselung
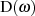 .6
Die zu approximierende Funktion
.6
Die zu approximierende Funktion 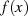 kann als Drosselung des (fast) idealen Tiefpaß verstanden
werden.
kann als Drosselung des (fast) idealen Tiefpaß verstanden
werden.
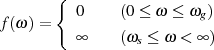
Genau an dieser Stelle unterscheiden sich nun die Standard-Tiefpässe dadurch, daß jeder Typ die
Zielfunktion 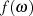 in anderen Frequenzbereichen approximiert. Abgesehen davon ist jede dieser
Bestapproximationen, welche ja als Zielgröße
in anderen Frequenzbereichen approximiert. Abgesehen davon ist jede dieser
Bestapproximationen, welche ja als Zielgröße 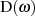 verwenden, auch eine in Bezug auf
verwenden, auch eine in Bezug auf 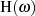 . Der
Grund ist in Ausgangsgleichung 2.1 zu finden, welche nur eine direkte Abhängigkeit
. Der
Grund ist in Ausgangsgleichung 2.1 zu finden, welche nur eine direkte Abhängigkeit 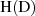 und keine
weitere von
und keine
weitere von 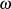 enthält. Aus diesem Grund unterscheiden sich zwar die Fehlerfunktion
enthält. Aus diesem Grund unterscheiden sich zwar die Fehlerfunktion 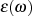 im Wert,
nicht aber im alternierenden Verhalten.
im Wert,
nicht aber im alternierenden Verhalten.
Geht man nun von einer Bestapproximation (wie in Abbildung 2.1 getan) aus, dann kann man den
Frequenz-Eckwerten 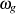 und
und 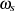 , da es sich um die Randpunkte handelt, die Dämpfungswerte
, da es sich um die Randpunkte handelt, die Dämpfungswerte 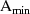 und
und 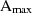 zuordnen.
zuordnen.

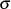 bestimmen.
bestimmen.