


Der erste Typ des TSCHEBYSCHEff-Tiefpaß ist durch direkte Anwendung der TSCHEBYSCHEff-Funktionen erster Art (siehe Anhang ??) für die Drosselung gekennzeichnet [Zve67, Che95, Fri79a].
Man kann sich auch leicht an Hand der folgenden Definition für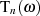 davon überzeugen, daß
die Funktion im Intervall
davon überzeugen, daß
die Funktion im Intervall 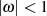 eine Bestapproximation der Nullinie (im Sinne von
Abschnitt 2.1.2, vgl. auch [Kör88, 45] oder [Mei64, § 4]) darstellt, für
eine Bestapproximation der Nullinie (im Sinne von
Abschnitt 2.1.2, vgl. auch [Kör88, 45] oder [Mei64, § 4]) darstellt, für 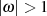 aber gegen
aber gegen 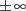 strebt.
strebt.

Daß es sich hier wirklich um Polynome in 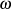 handelt, zeigt die äquivalente Definitionsgleichung ??
für
handelt, zeigt die äquivalente Definitionsgleichung ??
für 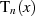 im Anhang ??. Dort sind auch TSCHEBYSCHEff-Polynome bis zum Grad
im Anhang ??. Dort sind auch TSCHEBYSCHEff-Polynome bis zum Grad 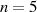 sowie ihr
Funktionsverlauf (in Abbildung ??) gegeben. Wie spezielle Werte des Funktionsverlaufs von
sowie ihr
Funktionsverlauf (in Abbildung ??) gegeben. Wie spezielle Werte des Funktionsverlaufs von 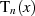 sich auf den normierten Amplitudengang nach
sich auf den normierten Amplitudengang nach
Die Grenzfrequenz ist bei diesem Tiefpaß-Typ immer normiert 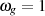 , zumindest soweit man sie als
Eckfrequenz entsprechend Tiefpaß-Toleranzfeld in Abbildung 2.1 sieht. Der Amplitudengang hat im
Durchlaßbereich eine Welligkeit, welche durch die TSCHEBYSCHEff-Funktion verursacht wird (vgl.
Abbildung ??). Sie nimmt an den Extremstellen
, zumindest soweit man sie als
Eckfrequenz entsprechend Tiefpaß-Toleranzfeld in Abbildung 2.1 sieht. Der Amplitudengang hat im
Durchlaßbereich eine Welligkeit, welche durch die TSCHEBYSCHEff-Funktion verursacht wird (vgl.
Abbildung ??). Sie nimmt an den Extremstellen 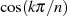 alternierend die Werte
alternierend die Werte 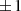 an –
dazwischen liegen (notwendigerweise) die Nullstellen bei
an –
dazwischen liegen (notwendigerweise) die Nullstellen bei ![cos[(k − 1∕2 )π ∕n]](stdfilter516x.png) . Kombiniert man beide
Ausdrücke, dann erhält man die Extremstellen des Amplitudengangs.
. Kombiniert man beide
Ausdrücke, dann erhält man die Extremstellen des Amplitudengangs.
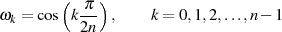
An diesen Stellen ist 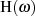 nach Tabelle 2.1 entweder
nach Tabelle 2.1 entweder 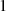 oder
oder 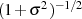 und die Welligkeit
und die Welligkeit  deshalb:
deshalb:
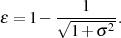
Wie schon beim BUTTERWORTH-Tiefpaß besteht ein determinierter Zusammenhang zwischen der Grenz- und Sperrfrequenz sowie der minimalen und maximalen Sperrdämpfung.
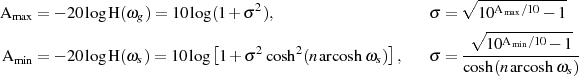
Aus diesen Abhängigkeiten kann man durch Gleichsetzen der Ausdrücke für 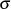 wieder den minimalen
Grad des Filters bestimmen.
wieder den minimalen
Grad des Filters bestimmen.
Um die Verteilung der Polstellen zu bestimmen, gehen wir von der komplexen Übertragungsfunktion
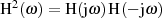 aus
aus
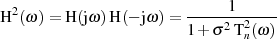
und verallgemeinern dann im Sinne der LAPLACE-Transformation 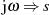 .
.
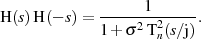
An den Polstellen muß der Nenner verschwinden, was heißt:
Wegen 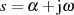 müssen wir davon ausgehen, daß
müssen wir davon ausgehen, daß 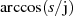 eine komplexe Größe ist. Um nicht
den Überblick zu verlieren substituieren wir
eine komplexe Größe ist. Um nicht
den Überblick zu verlieren substituieren wir 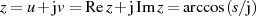 und notieren als
komplexe Gleichung:
und notieren als
komplexe Gleichung:
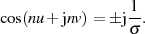
Nimmt man das Additionstheorem 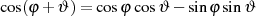 hinzu, dann sind die
Gleichungen
hinzu, dann sind die
Gleichungen
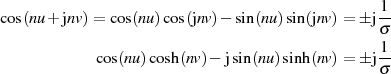
äquivalent und wir können die Nullstellenbedingung in Real- und Imaginärteil separieren.

Der Realteil wird Null, wenn 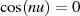 gilt, was für Argumente
gilt, was für Argumente 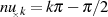 bzw.
bzw.
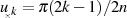 der Fall ist. Einsetzen in die imaginäre Bedingung führt zu
der Fall ist. Einsetzen in die imaginäre Bedingung führt zu
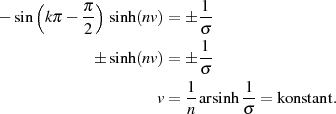
Mit diesen Ergebnissen kehren wir zur Substitution 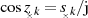 zurück und wenden (wieder) das
komplexe Additionstheorem
zurück und wenden (wieder) das
komplexe Additionstheorem 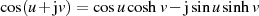 an.
an.
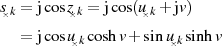
Einsetzen von  und
und  ergibt für die
ergibt für die  Polstellen der Funktion
Polstellen der Funktion 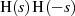 , getrennt für Real- und
Imaginärteil:
, getrennt für Real- und
Imaginärteil:
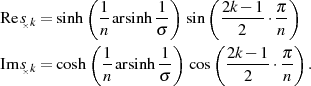
Interpretiert man beide Anteile geometrisch, dann ist zu bemerken, daß alle Pole auf einer Ellipse mit den Halbachsen
liegen (siehe auch Abbildung 2.5).14 Wegen der für Hyperbelfunktionen immer geltenden Äquivalenz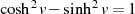 besteht
zwischen den Halbachsen die Abhängigkeitsbeziehung
besteht
zwischen den Halbachsen die Abhängigkeitsbeziehung 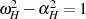 .
.
Abschließend wählen wir die Hälfte der  Pole, nämlich (aus Stabilitätsgründen) die mit negativem Realteil aus, und
ordnen sie
Pole, nämlich (aus Stabilitätsgründen) die mit negativem Realteil aus, und
ordnen sie 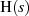 zu.15
zu.15