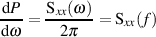Machen wir nun einen weiteren Schritt von den Zufallsprozessen zu
Zufallssignalen, der aber eher eine Notationsfrage als etwas Grundsätzliches
ist.29
Dabei stellen wir die Frage nach der spektralen Leistungsdichte eines stationären, ergodischen
Zufallsprozesses, also nach infinitesimalen Leistungsanteilen in einem Frequenzbereich 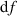 (bzw.
(bzw.
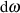 ), der einem Zufallssignal
), der einem Zufallssignal 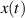 zugeordnet ist. Von Gleichung 53 wissen wir, daß für die
Gesamtleistung
zugeordnet ist. Von Gleichung 53 wissen wir, daß für die
Gesamtleistung 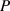 von
von 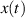 die Formel
die Formel
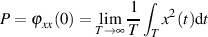
gilt. Aus dem Gebiet der Harmonischen Analyse ist außerdem bekannt, daß die spektrale
“Leistungsamplitude” an der (Kreis-) Frequenz 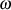 durch
durch 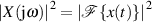 gekennzeichnet ist.
Die FOURIER-Transformation als uneigentliches Integral
gekennzeichnet ist.
Die FOURIER-Transformation als uneigentliches Integral
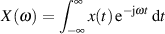
muß für die Existenz von 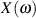 aber konvergieren, was man bei Zufallsprozessen wegen
aber konvergieren, was man bei Zufallsprozessen wegen
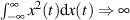 normalerweise nicht gewährleisten kann. Trotzdem kann man für diesen Fall
(mitunter durch Einsatz der DIRAC-Funktion) eine Größe entwickeln, die spektrale Leistungsdichte
normalerweise nicht gewährleisten kann. Trotzdem kann man für diesen Fall
(mitunter durch Einsatz der DIRAC-Funktion) eine Größe entwickeln, die spektrale Leistungsdichte
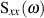 des Zufallsprozesses
des Zufallsprozesses 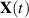 genannt wird. Dazu bilden wir die FOURIER-Transformierte der
Autokorrelationsfunktion
genannt wird. Dazu bilden wir die FOURIER-Transformierte der
Autokorrelationsfunktion
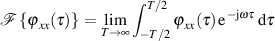
und ersetzen mit Hilfe von Formel 52 formal 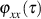 .
.
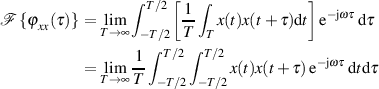
Nun wird die Integrationsreihenfolge vertauscht und danach 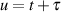 substituiert.30
substituiert.30
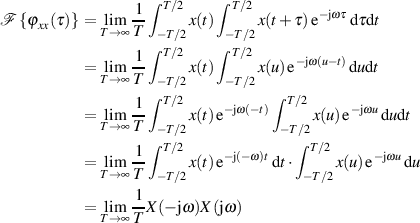
Auch wenn das FOURIER-Integral 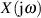 selbst nicht konvergiert,
so ist doch
selbst nicht konvergiert,
so ist doch 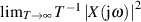 bzw.
bzw. 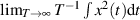 endlich.31
endlich.31
Man nennt den so gewonnen Ausdruck die spektrale Leistungsdichte 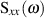 des
Zufallsprozesses bzw. das WIENER-CHINTCHIN-Theorem [Kan73, 7.2], [Sch90, 7.3].
Interessant ist auch, daß sich diese Gleichung (57) ganz einfach ergibt, wenn man den
Faltungssatz32
der Fourier-Transformation auf die Form der Autokorrelationsfunktion von Formel 55 anwendet.
des
Zufallsprozesses bzw. das WIENER-CHINTCHIN-Theorem [Kan73, 7.2], [Sch90, 7.3].
Interessant ist auch, daß sich diese Gleichung (57) ganz einfach ergibt, wenn man den
Faltungssatz32
der Fourier-Transformation auf die Form der Autokorrelationsfunktion von Formel 55 anwendet.
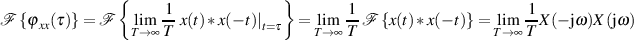
Die Grundaussage des Satzes von WIENER und CHINTCHIN, nämlich das die spektrale Leistungsdichte mit der Autokorrelationsfunktion über die FOURIER-Transformation verbunden ist, rechtfertigt natürlich auch die Umkehrformel:
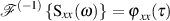
bzw. symbolische Darstellung der FOURIER-Transformation.
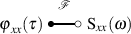
Die spektrale Leistungsdichte eines Zufallsprozesses hat einige interessante Eigenschaften:
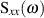 reelwertig und positiv sein.33
reelwertig und positiv sein.33
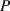 des stochastischen Prozesses kann durch Integration über die
gesamte spektrale Leistungsdichte
des stochastischen Prozesses kann durch Integration über die
gesamte spektrale Leistungsdichte 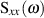 gewonnen werden.
gewonnen werden.
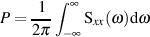
Für diesen Nachweis geht man am Besten von der bekannten Beziehung 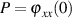 aus.
aus.
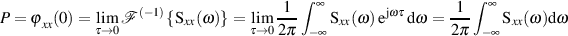
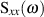 auch wirklich als Leistungsdichte auffassen, wenn man
den Hauptsatz der Differential- und Integralrechnung hinzuzieht.34
auch wirklich als Leistungsdichte auffassen, wenn man
den Hauptsatz der Differential- und Integralrechnung hinzuzieht.34