


Der BUTTERWORTH-Tiefpaß  -ter Ordnung zeichnet sich durch die Amplitudencharakteristik
-ter Ordnung zeichnet sich durch die Amplitudencharakteristik
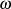 nur in der höchsten Potenz vorhanden ist, werden solche
Systeme auch Potenzfilter genannt und als maximal flach bezeichnet [Fri79a]
[Win54].7
Abbildung 2.2 zeigt den Amplitudengang nach Formel 2.4 für unterschiedlichen Grad
nur in der höchsten Potenz vorhanden ist, werden solche
Systeme auch Potenzfilter genannt und als maximal flach bezeichnet [Fri79a]
[Win54].7
Abbildung 2.2 zeigt den Amplitudengang nach Formel 2.4 für unterschiedlichen Grad
 .
.
Mit Hilfe des Parameters 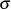 kann die maximale Dämpfung im Durchlaßbereich
kann die maximale Dämpfung im Durchlaßbereich 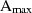 variiert werden
(vgl. Abschnitt 2.1.1). Dazu sei von der normierten Grenzfrequenz
variiert werden
(vgl. Abschnitt 2.1.1). Dazu sei von der normierten Grenzfrequenz 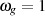 ausgegangen, bei
der
ausgegangen, bei
der
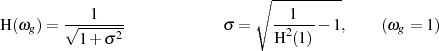
gilt und deshalb für die maximale Dämpfung:
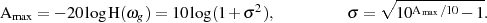
In gleicher Art und Weise kann man für die minimale Dämpfung im Sperrbereich
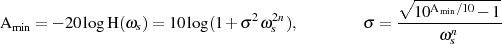
erhalten, d. h. die charakteristischen Größen 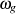 ,
, 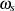 ,
, 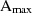 und
und 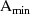 sind nicht unabhängig
voneinander. Der über den Grad
sind nicht unabhängig
voneinander. Der über den Grad  bestehende Zusammenhang kann durch Gleichsetzen der
Beziehungen für
bestehende Zusammenhang kann durch Gleichsetzen der
Beziehungen für 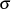 ausgedrückt werden.
ausgedrückt werden.
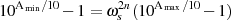
Aus dieser Äquivalenz kann der minimale Grad eines BUTTERWORTH-Tiefpaß’ ausgehend von den
charakteristischen Größen abgeleitet werden (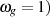 .
.
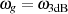 , d. h. auf
, d. h. auf 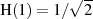 ,
dimensioniert. Dann gilt
,
dimensioniert. Dann gilt 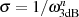 und für den Amplitudengang
und für den Amplitudengang
Die Verteilung der Polstellen eines Filters (in der komplexen Ebene) ist grundsätzlich immer
interessant, da sie Aufschlüsse bezüglich der anderen Charakteristiken, wie Amplitudengang,
Phasengang, usw. zuläßt. Dazu gehen wir von der komplexen Übertragungsfunktion 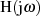 , in
Verbindung mit der generellen Eigenschaft
, in
Verbindung mit der generellen Eigenschaft 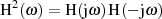 , aus.
, aus.
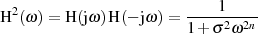
Der Übergang in den LAPLACE-Bereich (mit 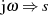 ) führt
zu:8
) führt
zu:8
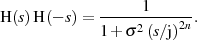 | (2.8) |
An den Polstellen von 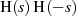 muß der Nenner in Gleichung 2.8 verschwinden, was
bedeutet:
muß der Nenner in Gleichung 2.8 verschwinden, was
bedeutet:
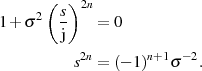
Die komplexen  Wurzeln lassen sich mit Hilfe des Satzes von MOIVRE sofort
angeben:9
Wurzeln lassen sich mit Hilfe des Satzes von MOIVRE sofort
angeben:9

Um realisierbare Systeme zu erhalten ordnet man nun  Pole mit negativem Realteil
Pole mit negativem Realteil 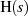 , die
anderen
, die
anderen 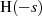 zu. Man erhält, was sich durch Einsetzen einzelner Werte
zu. Man erhält, was sich durch Einsetzen einzelner Werte 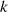 leicht nachprüfen läßt,
folgende Polverteilung für einen BUTTERWORTH-Tiefpaß.
leicht nachprüfen läßt,
folgende Polverteilung für einen BUTTERWORTH-Tiefpaß.
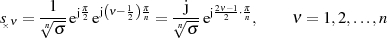 | (2.9) |
Sind insbesondere Real- oder Imaginärteile von Interesse, dann ist auf Gleichung 2.9 noch die EULER’sche Formel anzuwenden.
Anschaulich liegen alle Pole auf einem Kreis mit Radius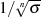 , was deutlich auch
in Abbildung 2.3 zu erkennen ist. Außerdem zeigt die Darstellung, daß einerseits
keine Pole auf der imaginären Achse liegen und andererseits alle konjugiert komplex
auftreten.10
, was deutlich auch
in Abbildung 2.3 zu erkennen ist. Außerdem zeigt die Darstellung, daß einerseits
keine Pole auf der imaginären Achse liegen und andererseits alle konjugiert komplex
auftreten.10
Allgemein gelten Polkenngrößen als geeignet zur Abschätzung des Systemverhaltens im Frequenzbereich. Dabei
sind es vor allem zwei Größen, die entsprechende Bedeutung erlangt haben – die Polfrequenz 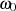 und die
Polgüte
und die
Polgüte 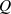 .11
Zur Definition bzw. Bestimmung geht man von der Erkenntnis aus, daß komplexe Pole immer
konjugiert auftreten und deshalb in der Linearfaktordarstellung von
.11
Zur Definition bzw. Bestimmung geht man von der Erkenntnis aus, daß komplexe Pole immer
konjugiert auftreten und deshalb in der Linearfaktordarstellung von 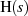 paarweise (zur Vermeidung
komplexer Größen) zusammengefaßt werden können.
paarweise (zur Vermeidung
komplexer Größen) zusammengefaßt werden können.
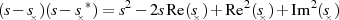
Dieses Polynom zweiten Grades (bezüglich der LAPLACE-Variable  ) kann man auch folgendermaßen
schreiben
) kann man auch folgendermaßen
schreiben
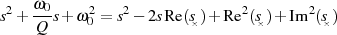
führt sofort zur Definition der Polfrequenz 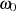 als Betragswert der jeweiligen Polstelle
als Betragswert der jeweiligen Polstelle
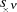 .
.
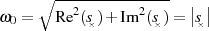 | (2.12) |
Die Polgüte 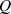 ist nicht sofort ablesbar, kann aus
ist nicht sofort ablesbar, kann aus
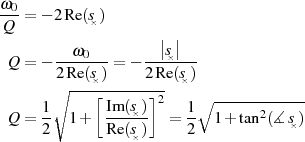
aber ohne größeren Aufwand bestimmt werden:12
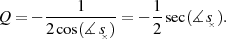 | (2.13) |
Speziell für einen BUTTERWORTH-Tiefpaß gilt deshalb in Bezug auf die Polfrequenzen:
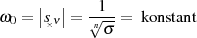
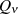 für höhere Filterordnung
für höhere Filterordnung
 immer größer werden, wobei Pole in der Nähe der
immer größer werden, wobei Pole in der Nähe der 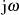 -Achse die höchsten Güten
aufweisen.13
-Achse die höchsten Güten
aufweisen.13