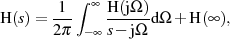Für Systeme der realen Welt kann man grundsätzlich davon ausgehen, daß es eine Wirkung vor der
Ursache ausgeschlossen ist. Man fordert deshalb von einem so charakterisierten LTI-System, daß für
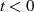 das Ausgangssignal
das Ausgangssignal 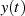 verschwindet. Aus systemtheoretischer Sicht kann eine derartige
Einschränkung an die Zeitfunktion nicht ohne Einfluß auf die Bildfunktion der FOURIER-
bzw. LAPLACE-Transformation bleiben. Welche Forderungen an die Transformierte eines
kausalen Signals
verschwindet. Aus systemtheoretischer Sicht kann eine derartige
Einschränkung an die Zeitfunktion nicht ohne Einfluß auf die Bildfunktion der FOURIER-
bzw. LAPLACE-Transformation bleiben. Welche Forderungen an die Transformierte eines
kausalen Signals 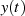 unter dieser Bedingung zu stellen sind, soll im Folgenden ermittelt
werden.
unter dieser Bedingung zu stellen sind, soll im Folgenden ermittelt
werden.
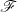 -Bildfunktion
-BildfunktionDer geradlinigste Ansatz formuliert das Verschwinden des Signals 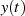 für
für 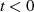 durch die
Äquivalenz
durch die
Äquivalenz
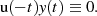
FOURIER-Transformation dieser (notwendigen, für realisierbare Systeme nicht
hinreichenden) Bedingung in den Bildbereich führt mit Hilfe des Faltungssatzes
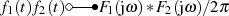 sowie der Korrespondenz
sowie der Korrespondenz 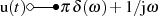 zu:6
zu:6
![Y(jω ) [ 1] 1 [ 1 ]
-----∗ πδ(− ω) +j-- = -- Y(jω )+ j---∗ Y(jω ) = 0.
2π ω 2 πω](stdfilter105x.png)
Separiert man Real- und Imaginärteil, dann muß für ein kausales Signal
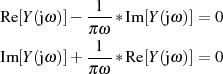
gelten. Umstellen nach 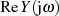 und
und 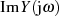 ergibt folgende Zusammenhänge:
ergibt folgende Zusammenhänge:
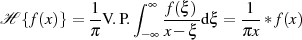
Ein anderer, aber sehr einfacher Ansatz geht davon aus, daß grundsätzlich jede Zeitfunktion in eine
gerade und eine ungerade Teilfunktion 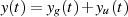 zerlegt werden kann [Pap62, 10-2],
[Fri85, 4.1]. Dann gilt wegen
zerlegt werden kann [Pap62, 10-2],
[Fri85, 4.1]. Dann gilt wegen 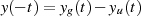 bei Addition und Subtraktion beider
Formeln:
bei Addition und Subtraktion beider
Formeln:

d. h. beide Teilfunktionen sind von 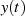 und deshalb auch wechselseitig
abhängig.8
Im speziellen Fall eines kausalen Signals, d. h.
und deshalb auch wechselseitig
abhängig.8
Im speziellen Fall eines kausalen Signals, d. h. 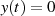 für
für 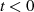 bzw.
bzw. 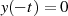 für
für  kann
folgendermaßen vereinfacht werden:
kann
folgendermaßen vereinfacht werden:
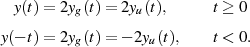
Hieraus läßt sich die Abhängigkeit zwischen geradem und ungeradem Anteil von 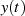 direkt
ablesen.
direkt
ablesen.

Berücksichtigt man jetzt noch die Eigenschaft der FOURIER-Transformation reeller Zeitfunktion,
nämlich daß der gerade Anteil von 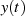 mit dem Realteil der Bildfunktion
mit dem Realteil der Bildfunktion 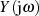 , der ungerade Teil
hingegen mit dem Imaginärteil korrespondiert (vgl. ??), so führt Anwendung des Faltungssatzes
, der ungerade Teil
hingegen mit dem Imaginärteil korrespondiert (vgl. ??), so führt Anwendung des Faltungssatzes
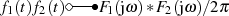 sowie der Korrespondenz
sowie der Korrespondenz  zum bekannten
Ergebnis:
zum bekannten
Ergebnis:

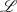 -Bildfunktion
-BildfunktionNehmen wir als Ausgangssituation der Betrachtungen in der LAPLACE-Ebene an, daß
die Transformierte 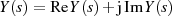 des reellen Signals
des reellen Signals 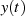 in der rechten
Halbebene vollständig analytisch sei, d. h. dort weder Singularitäten (also auch keine Pole)
noch Sprünge hat. Aus der Funktionentheorie ist bekannt, daß sich eine solche Funktion
(unter der Bedingung
in der rechten
Halbebene vollständig analytisch sei, d. h. dort weder Singularitäten (also auch keine Pole)
noch Sprünge hat. Aus der Funktionentheorie ist bekannt, daß sich eine solche Funktion
(unter der Bedingung 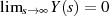 , vgl. Abschnitt ?? oder [Pap62, 10-5]) für
, vgl. Abschnitt ?? oder [Pap62, 10-5]) für
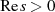 vollständig durch ihre Randwerte auf der imaginären Achse definiert [BC03,
119].9
vollständig durch ihre Randwerte auf der imaginären Achse definiert [BC03,
119].9
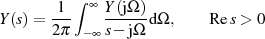 | (1.12) |
Aus demselben mathematischen Gebiet entstammen auch die folgenden Ausdrucksmöglichkeiten,
welche für 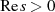 die Rückgewinnung der Funktion nur aus dem Real- oder Imaginärteil
ermöglichen.
die Rückgewinnung der Funktion nur aus dem Real- oder Imaginärteil
ermöglichen.
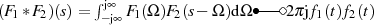 an [AS72, 29], wobei
an [AS72, 29], wobei 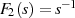 und
und 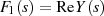 bzw.
bzw. 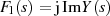 gesetzt
wird.
gesetzt
wird.
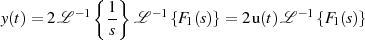 | (1.14) |
Diese Beziehung enthält das wesentliche Resultat: wegen der Multiplikation mit dem Einheitssprung 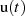 verschwindet das Signal
verschwindet das Signal 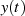 für
für 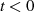 (Kausalität), wenn
(Kausalität), wenn 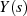 in der gesamten rechten Halbebene analytisch
ist.10
in der gesamten rechten Halbebene analytisch
ist.10
Die Aussage führt zu einer wesentlichen Forderung an die Übertragungsfunktion eines LTI-Systems
(wenn 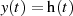 und demzufolge
und demzufolge 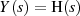 gesetzt wird), nämlich daß eine rationale
gesetzt wird), nämlich daß eine rationale
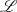 -Übertragungsfunktion
-Übertragungsfunktion 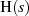 keine Pole in der rechten Halbebene besitzen darf.
keine Pole in der rechten Halbebene besitzen darf.
Anhand der vorangegangenen Ausführungen wurde deutlich, daß ein kausales Signal (bzw. die
Impulsantwort eines LTI-Systems) unbedingt mit einer Abhängigkeit zwischen Real- und Imaginärteil
der Bildfunktion (über die HILBERT-Transformation) verbunden ist. Aus der Funktionentheorie
entstammte die weiterreichende Erkenntnis, daß ein solcher Zusammenhang immer dann gegeben ist,
wenn sich das Signal in der rechten 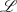 -Halbebene als frei von Singularitäten darstellt. Für die
Übertragungsfunktion eines LTI-Systems hat deshalb die Lage der Pole entscheidende Bedeutung nicht
nur in Bezug auf die Stabilität sondern auch auf die Kausalität der Impulsantwort und damit die
Realisierbarkeit.
-Halbebene als frei von Singularitäten darstellt. Für die
Übertragungsfunktion eines LTI-Systems hat deshalb die Lage der Pole entscheidende Bedeutung nicht
nur in Bezug auf die Stabilität sondern auch auf die Kausalität der Impulsantwort und damit die
Realisierbarkeit.
Was die kausalen Signale angeht, so kann man aufgrund der Abhängigkeit zwischen Real- und Imaginärteil noch redundanzfreie Darstellungen ableiten [Bra03, 13]:
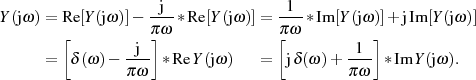
Durch Anwendung des Faltungssatzes und (wieder) der Transformation für den Einheitssprung sowie
![∫ ∞ δ(ω − Ω) Re[Y (jΩ )]dΩ = Re Y(jω)
− ∞](stdfilter161x.png) auf
auf
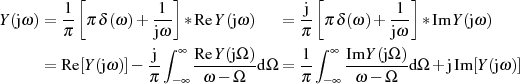
erhält man für die Zeitfunktion
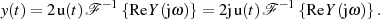
Sollte 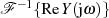 für
für  verschwinden, dann ist es also ausreichend nur eine
Komponente, entweder Real- oder Imaginärteil, zur Beschreibung des Signals
verschwinden, dann ist es also ausreichend nur eine
Komponente, entweder Real- oder Imaginärteil, zur Beschreibung des Signals 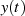 heranzuziehen.11
heranzuziehen.11
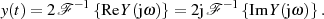 | (1.15) |
Die jeweils andere Komponente ist faktisch redundant, was solche Transformationen wie die Cosinus- oder Sinus-Transformation rechtfertigt [Wun62, 3.2], [Sto92, 5.1.2]. Diese ergeben sich (bis auf einen konstanten Faktor) sofort aus Formel 1.15, wenn man die Symmetrieeigenschaften der trigonometrischen Funktionen berücksichtigt.
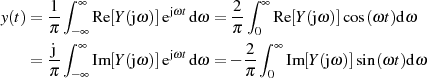
In gleicher Art und Weise können auch die Ausführungen für die LAPLACE-Transformierte 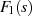 von
Seite 23 fortgesetzt werden. Denn gehorcht
von
Seite 23 fortgesetzt werden. Denn gehorcht 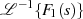 der Bedingung nach Gleichung 1.14 “von
Hause aus”, d. h. verschwindet für
der Bedingung nach Gleichung 1.14 “von
Hause aus”, d. h. verschwindet für 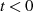 , so wird wegen des Wegfalls des jetzt unnötigen
Faktors
, so wird wegen des Wegfalls des jetzt unnötigen
Faktors 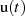 das kausale Signal
das kausale Signal 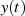 vollständig durch den Real- oder Imaginärteil seiner
LAPLACE-Transformierten beschrieben.
vollständig durch den Real- oder Imaginärteil seiner
LAPLACE-Transformierten beschrieben.
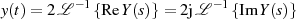 | (1.16) |
Berücksichtigt man die Eigenschaften der FOURIER- bzw. LAPLACE-Transformierten reeller Zeitfunktionen, so lassen sich für die Übertragungsfunktion von kausalen LTI-Systemen zahlreiche Darstellungsformen angeben, die oftmals als Integralsätze von BODE bezeichnet werden [Bod45], [Mar95, 5.1], [Pap62, 10.], [SBG97, 2.3.2].
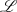 -Ebene
-EbeneEine erste Betrachtung dazu (die etwas ausführlicher erfolgt), geht von Formel 1.12 aus und erweitert
zunächst den Integranden mit 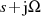 .
.
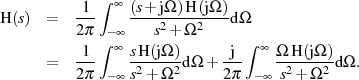
Bedenkt man nun, daß:
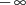 bis
bis  über eine ungerade Funktion Null ergibt;
über eine ungerade Funktion Null ergibt;
![[0,∞]](stdfilter181x.png) ausgedrückt werden kann;
ausgedrückt werden kann;
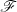 -Transformierten einer reellen Zeitfunktion eine ungerade
Funktion ist;
-Transformierten einer reellen Zeitfunktion eine ungerade
Funktion ist;
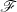 -Transformierten einer reellen Zeitfunktion eine gerade Funktion ist;
-Transformierten einer reellen Zeitfunktion eine gerade Funktion ist;
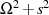 als auch
als auch 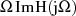 bezüglich der Integrationsvariable
bezüglich der Integrationsvariable  gerade
Funktionen sind;
gerade
Funktionen sind;
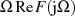 hingegen eine ungerade Funktion darstellt;
hingegen eine ungerade Funktion darstellt;so ergibt sich im 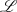 -Bildbereich:
-Bildbereich:
![∫ ∞
H(s)= 1- sRe[H(jΩ-)]−-ΩIm-[H-(jΩ-)]d Ω, Re s> 0.
π 0 s2+ Ω2](stdfilter189x.png)
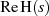 im Zähler des Integrals
im Zähler des Integrals
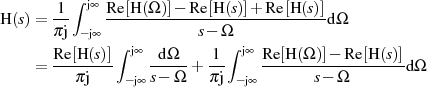
und nimmt die für 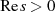 geltende Beziehung
geltende Beziehung 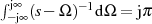 zu Hilfe.
zu Hilfe.
![1∫ j∞ Re[H(Ω )]− Re[H (s)]
H(s)= Re [H (s)]+ πj ------s−-Ω--------dΩ
− j∞](stdfilter194x.png)
Bringt man noch 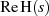 auf die linke Seite, so kann direkt eine neue Variante
der Abhängigkeitsdarstellung zwischen Real- und Imaginärteil gewonnen
werden.12
auf die linke Seite, so kann direkt eine neue Variante
der Abhängigkeitsdarstellung zwischen Real- und Imaginärteil gewonnen
werden.12
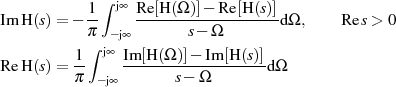
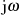 -Achse
-AchseAuf der imaginären Achse gilt (für Systeme mit 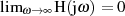 , vgl. Abschnitt ??) die aus der
Funktionentheorie bekannte Beziehung:
, vgl. Abschnitt ??) die aus der
Funktionentheorie bekannte Beziehung:
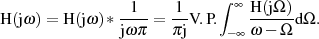 | (1.17) |
Mit dem Ziel den Nenner des Integranden zu einer geraden (oder ungeraden) Funktion zu machen, soll
uns  als Erweiterung dienen.
als Erweiterung dienen.
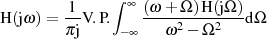
Dabei verschwinden die Integrale über 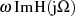 und
und 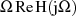 , da es sich bezüglich
, da es sich bezüglich  um
ungerade Funktionen handelt.
um
ungerade Funktionen handelt.
Oftmals sind in der Literatur Darstellungen zu finden, in denen 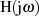 auch auf der rechten Seite im
Integranden auftaucht und die letztlich auf [Bod45] zurückgehen [Pap62, 10-2], [Wun62, 3.14], [Spǎ73,
6.4].14
auch auf der rechten Seite im
Integranden auftaucht und die letztlich auf [Bod45] zurückgehen [Pap62, 10-2], [Wun62, 3.14], [Spǎ73,
6.4].14
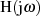 aus dem Integral herausgezogen werden, da er nicht von der
Integrationsvariable
aus dem Integral herausgezogen werden, da er nicht von der
Integrationsvariable  abhängt. Unsere Aufmerksamkeit soll deshalb dem Integral
abhängt. Unsere Aufmerksamkeit soll deshalb dem Integral 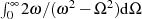 gelten,15
dessen CAUCHY’scher Hauptwert sowohl anschaulich als auch im
Hinblick auf dessen Stammfunktion
gelten,15
dessen CAUCHY’scher Hauptwert sowohl anschaulich als auch im
Hinblick auf dessen Stammfunktion 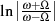 verschwindet [AS72,
3.3.23].16
verschwindet [AS72,
3.3.23].16
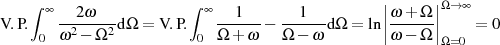
Beide Beziehungen entsprechen folglich den Formeln 1.19 und 1.20, nutzen also nur die Äquivalenz:
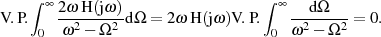
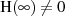
Für LTI-Systeme mit der Eigenschaft
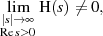
aber mit beschränkter 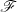 -Übertragungsfunktion
-Übertragungsfunktion 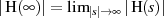 , wie für rationale
Übertragungsfunktionen in Abschnitt 1.3 betrachtet, kann man nicht auf JORDAN’s Lemma
zurückgreifen. Aus diesem Grund sind alle vorangegangenen Aussagen derart anzupassen, daß der im
Unendlichen verlaufende Integrationsweg (nach Abbildung ??) bei der Anwendung von CAUCHY’s
Integralformel berücksichtigt wird [Wun62, 3.12], [Pap62, 10-2]. Den allgemeinen Fall
einer, in der rechten Halbebene analytischen Funktion, muß man deshalb folgendermaßen
korrigieren:
, wie für rationale
Übertragungsfunktionen in Abschnitt 1.3 betrachtet, kann man nicht auf JORDAN’s Lemma
zurückgreifen. Aus diesem Grund sind alle vorangegangenen Aussagen derart anzupassen, daß der im
Unendlichen verlaufende Integrationsweg (nach Abbildung ??) bei der Anwendung von CAUCHY’s
Integralformel berücksichtigt wird [Wun62, 3.12], [Pap62, 10-2]. Den allgemeinen Fall
einer, in der rechten Halbebene analytischen Funktion, muß man deshalb folgendermaßen
korrigieren:
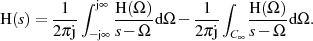 | (1.23) |
Betrachten wir zuerst den Integrationsweg 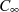 und bringen die Substitution
und bringen die Substitution 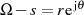 mit
mit
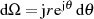 zur Anwendung.
zur Anwendung.
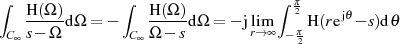
Unter der Maßgabe 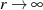 kann man sicherlich
kann man sicherlich 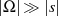 annehmen, d. h.
annehmen, d. h. 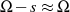 setzen.
setzen.
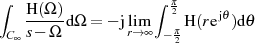
Außerdem ist wegen der (für reelle Zeitfunktionen immer geltenden) Relation
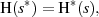
eine Beschränkung des Integrationsweges auf einen positiven Viertelkreis möglich.
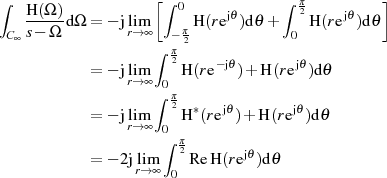
Letzter Ausdruck weist nun eindeutig darauf hin, daß es sich bei dem Integral entlang 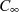 um eine rein imaginäre Konstante handelt, welche für
um eine rein imaginäre Konstante handelt, welche für 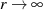 sowohl allgemein als auch
speziell auf der reellen Achse (
sowohl allgemein als auch
speziell auf der reellen Achse (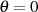 ,
, 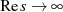 ) nicht notwendigerweise verschwinden
muß.
) nicht notwendigerweise verschwinden
muß.
Zurück zur Ausgangsbeziehung 1.23 erhalten wir durch Einsetzen
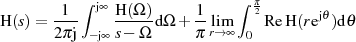
und stellen fest, daß sich der Realteil17
von 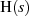 um den konstanten Betrag
um den konstanten Betrag
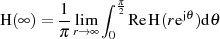
erhöht.18 Aus diesem Grund ändert sich z. B. Formel 1.12 wiefolgt: