


Minimalphasig nennt man Systeme, die in der rechten 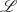 -Halbebene weder Pole noch Nullstellen
besitzen [Pap62, 10-3]. Für rationale Übertragungsfunktionen bedeutet diese Eigenschaft, daß
Nenner und Zähler von
-Halbebene weder Pole noch Nullstellen
besitzen [Pap62, 10-3]. Für rationale Übertragungsfunktionen bedeutet diese Eigenschaft, daß
Nenner und Zähler von 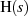 HURWITZ-Polynome sein müssen. Die Freiheit von Polen bzw.
Nullstellen für
HURWITZ-Polynome sein müssen. Die Freiheit von Polen bzw.
Nullstellen für 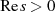 machen
machen 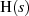 und
und 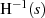 auf diesem Gebiet zu analytischen
Funktionen.20
Unter solchen Voraussetzungen ist man in der Lage,
auf diesem Gebiet zu analytischen
Funktionen.20
Unter solchen Voraussetzungen ist man in der Lage, 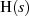 zu logarithmieren und dabei
die Holomorphieeigenschaft trotzdem zu bewahren. Bezeichnen wir
zu logarithmieren und dabei
die Holomorphieeigenschaft trotzdem zu bewahren. Bezeichnen wir 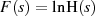 , so
kann man nach Beziehung 1.10 und 1.11 einen determinierten Zusammenhang zwischen
Dämpfung
, so
kann man nach Beziehung 1.10 und 1.11 einen determinierten Zusammenhang zwischen
Dämpfung 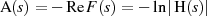 und Phase
und Phase 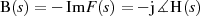 angeben.21
angeben.21

Eine wichtige Voraussetzung für die Anwendbarkeit beider Formeln ist nach dem Lemma von JORDAN
allerdings 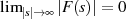 . Im Allgemeinen kann man von dieser Voraussetzung jedoch nicht
ausgehen, so daß genau wie in den Beziehungen 1.24 die Dämpfung
. Im Allgemeinen kann man von dieser Voraussetzung jedoch nicht
ausgehen, so daß genau wie in den Beziehungen 1.24 die Dämpfung 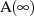 zu berücksichtigen
ist [Fri81, 5.3.1.2].
zu berücksichtigen
ist [Fri81, 5.3.1.2].

Praktisch kann man jedes LTI-System mit rationaler Übertragungsfunktion 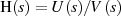 als Kettenschaltung eines Allpaß- und eines Minimalphasensystems verstehen [Pap62,
10-3], [Mar95, 5.2], [Wun62, 3.14], [Fri79a, 3.5]. Spalten wir dazu die Zählerfunktion
als Kettenschaltung eines Allpaß- und eines Minimalphasensystems verstehen [Pap62,
10-3], [Mar95, 5.2], [Wun62, 3.14], [Fri79a, 3.5]. Spalten wir dazu die Zählerfunktion 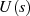 so auf, daß alle Nullstellen mit negativem Realteil in
so auf, daß alle Nullstellen mit negativem Realteil in 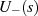 liegen, die mit positivem in
liegen, die mit positivem in
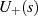 .
.
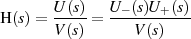
Einfache Erweiterung mit dem HURWITZ-Polynom 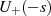 ergibt
ergibt
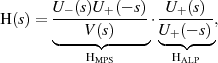 | (1.25) |
d. h. die Zerlegung in
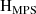 , welches keine Nullstellen in der rechten
, welches keine Nullstellen in der rechten 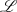 -Halbebene
besitzt;22
-Halbebene
besitzt;22
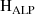 , also ein System mit
, also ein System mit 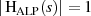 .
.
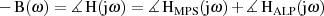
betrachtet. Denn würde der Anteil des Allpaß’ vermieden, so reduzierte sich das Gesamtsystem auf ein Minimalphasensystem.
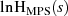 und
und 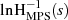 in der rechten
in der rechten 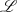 -Halbebene). Die Abhängigkeit von
Real- und Imaginärteil der einzelnen Übertragungsfunktion (vgl. Abschnitt 1.4) ist davon
thematisch unberührt, zumal sich die dadurch bedingte Kausalität und Stabilität auf die
Lage der Polstellen bezieht.
-Halbebene). Die Abhängigkeit von
Real- und Imaginärteil der einzelnen Übertragungsfunktion (vgl. Abschnitt 1.4) ist davon
thematisch unberührt, zumal sich die dadurch bedingte Kausalität und Stabilität auf die
Lage der Polstellen bezieht.
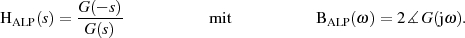
Um die Problematik etwas anschaulicher zu gestalten, hier ein Beispiel aus [Pap62, 10-3].

Wie sofort erkennbar, handelt es sich um ein stabiles System mit den Polen 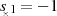 und
und
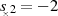 . Die Nullstelle des Allpaß’ bei
. Die Nullstelle des Allpaß’ bei 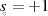 hat einen positiven Realteil, ist also
hat einen positiven Realteil, ist also
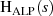 richtig zugeordnet. Obwohl insgesamt
richtig zugeordnet. Obwohl insgesamt 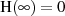 gilt (JORDAN-Bedingung),
verschwindet die Amplitude des Allpaß-Anteils
gilt (JORDAN-Bedingung),
verschwindet die Amplitude des Allpaß-Anteils 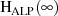 im Unendlichen
nicht.23
Auch die Partialbruchzerlegung für
im Unendlichen
nicht.23
Auch die Partialbruchzerlegung für 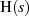 deutet einerseits auf Stabilität (speziell auch
deutet einerseits auf Stabilität (speziell auch 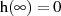 ),
andererseits auch auf Kausalität (
),
andererseits auch auf Kausalität (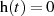 für
für 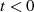 ) hin.
) hin.
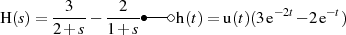
Beide als Kettenschaltungen anzusehende Übertragungsfunktionen
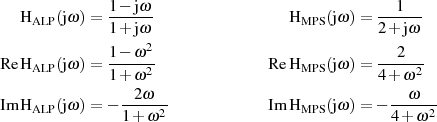
haben voneinander abhängige Real- und Imaginärteile, wie man mit der Transformationsbeziehung
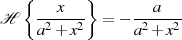
feststellt.
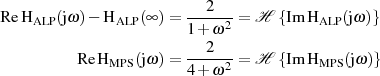
Trotzdem besteht ein fester Zusammenhang zwischen Dämpfungs- und Phaseverlauf nur für den
Minimalphasenteil 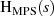 , nicht für
, nicht für 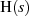 insgesamt. Der Allpaß-Anteil sorgt insbesondere dafür,
daß sich die Phase um den Betrag
insgesamt. Der Allpaß-Anteil sorgt insbesondere dafür,
daß sich die Phase um den Betrag 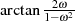 erhöht.
erhöht.