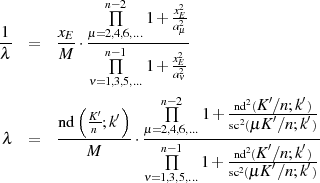Da hier genau die gleichen Bedingungen wie für den Fall ungerader Ordnung  gelten (vgl.
Abbildung 18), sind die meisten Beziehungen ähnlich. Einziger Unterschied besteht generell
darin, daß der Grad von Zähler- und Nennerpolynom entsprechend angepaßt werden muß.
gelten (vgl.
Abbildung 18), sind die meisten Beziehungen ähnlich. Einziger Unterschied besteht generell
darin, daß der Grad von Zähler- und Nennerpolynom entsprechend angepaßt werden muß.
Der Grad des Nennerpolynoms ist  , der des Zählerpolynoms
, der des Zählerpolynoms 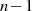 , was dazu führt, daß sich die
Funktion für
, was dazu führt, daß sich die
Funktion für  der Nullinie nähert. Dieses Verhalten ist auch im zugehörigen Funktionsverlauf
nach Abbildung 20 gut zu erkennen.
der Nullinie nähert. Dieses Verhalten ist auch im zugehörigen Funktionsverlauf
nach Abbildung 20 gut zu erkennen.
Die Koeffizienten bestimmen sich genauso wie für den Fall ungerader Ordnung  , also wie in
Formel 152, zu
, also wie in
Formel 152, zu
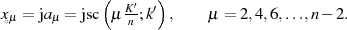
Gleiches gilt für den Multiplikator 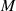 , für den ebenfalls nur der Grad von Zähler und Nenner in
Gleichung 155 zu korrigieren ist.
, für den ebenfalls nur der Grad von Zähler und Nenner in
Gleichung 155 zu korrigieren ist.
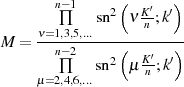
Anders beim Modul 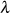 , welches (im Gegensatz zum Fall des ungeraden
, welches (im Gegensatz zum Fall des ungeraden  ) hier nicht durch
Evaluation der rationalen Transformationsbeziehung an der Stelle
) hier nicht durch
Evaluation der rationalen Transformationsbeziehung an der Stelle 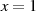 ermittelt werden kann.
Wegen der jetzt geraden Ordnung
ermittelt werden kann.
Wegen der jetzt geraden Ordnung  ist der Funktionswert dort nämlich
ist der Funktionswert dort nämlich 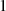 ist und nicht
ist und nicht
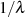 (vgl. Abbildung 18). Der Wert
(vgl. Abbildung 18). Der Wert 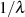 wird hingegen an den Extremstellen, d. h. bei
wird hingegen an den Extremstellen, d. h. bei
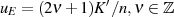 angenommen. Es ist also naheliegend einfach einen dieser Werte
angenommen. Es ist also naheliegend einfach einen dieser Werte 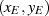 in Beziehung 157 einzusetzen.
in Beziehung 157 einzusetzen.