


Typisch für die 2. elliptische Transformation ist, daß die imaginäre Periode 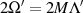 von
von
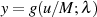 genau
genau  -mal die imaginäre Periode
-mal die imaginäre Periode  von
von  teilt, die reellen
Perioden aber gleich sind (
teilt, die reellen
Perioden aber gleich sind ( -te Teilung der imaginären Periode, vgl. Fall
-te Teilung der imaginären Periode, vgl. Fall 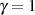 ,
, 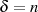 in
Abschnitt 4.5). Es handelt sich bei der Beziehung
in
Abschnitt 4.5). Es handelt sich bei der Beziehung 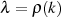 also ebenfalls um eine Modulgleichung
vom Grad
also ebenfalls um eine Modulgleichung
vom Grad  mit dem zugehörigen Periodenverhältnis
mit dem zugehörigen Periodenverhältnis
Allerdings kommt wegen  nur der Wert
nur der Wert 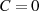 für die Integrationskonstante (vgl. Abschnitt 4.5)
in Frage, damit reelle Funktionswerte auf Wegabschnitt
für die Integrationskonstante (vgl. Abschnitt 4.5)
in Frage, damit reelle Funktionswerte auf Wegabschnitt  in Abbildung 8a bzw. nach Tabelle 5
entstehen.
in Abbildung 8a bzw. nach Tabelle 5
entstehen.
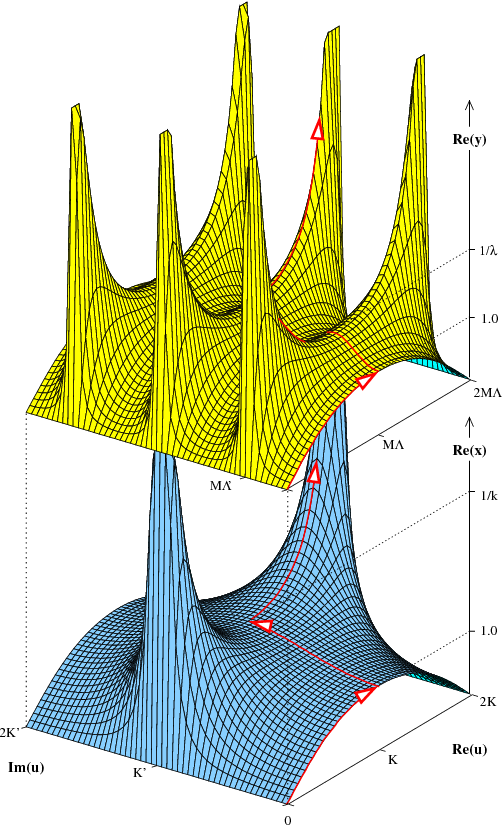
 )
)Der Funktionsverlauf 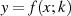 kann mit Hilfe von Abbildung 18 aus dem Verlauf des
Parameters
kann mit Hilfe von Abbildung 18 aus dem Verlauf des
Parameters  entsprechend der, in Abbildung 8a definierten, Wegabschnitte erklärt werden.
Auf Abschnitt
entsprechend der, in Abbildung 8a definierten, Wegabschnitte erklärt werden.
Auf Abschnitt  verlaufen
verlaufen  und
und 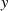 ausgehend vom Ursprung im Wesen gleich. Da im
Intervall
ausgehend vom Ursprung im Wesen gleich. Da im
Intervall 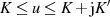 , d. h. auf Teilstück
, d. h. auf Teilstück  , die imaginäre Halbperiode
, die imaginäre Halbperiode 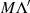 von
von
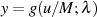
 -mal durchlaufen wird, existieren dort keine reellen Nullstellen oder Pole.
Statt dessen alterniert
-mal durchlaufen wird, existieren dort keine reellen Nullstellen oder Pole.
Statt dessen alterniert 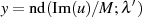 auf dem Weg
auf dem Weg 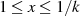 genau
genau 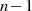 mal
zwischen
mal
zwischen  und
und 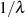 . Auf dem letzten Teilabschnitt
. Auf dem letzten Teilabschnitt  strebt
strebt 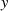 dann kontinuierlich gegen
dann kontinuierlich gegen
 .
.
Der resultierende Funktionsverlauf 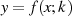 ist in Abbildung 19 dargestellt.
ist in Abbildung 19 dargestellt.
Die Form der rationalen Lösungsfunktion  für die zweite elliptische Haupttransformation
bei ungeradem Grad
für die zweite elliptische Haupttransformation
bei ungeradem Grad  kann ausgehend von Abbildung 18 sowie den folgenden Überlegungen
abgeleitet werden.
kann ausgehend von Abbildung 18 sowie den folgenden Überlegungen
abgeleitet werden.
 sowie
sowie  weitere bei jeweils
weitere bei jeweils 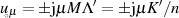 ,
, 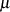 gerade.
gerade.
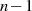 Pole liegen bei
Pole liegen bei 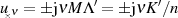 ,
,  ungerade.
ungerade.
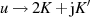 geht
geht  gegen Unendlich, was sich im Grad von Zähler- und
Nennerpolynom widerspiegelt (
gegen Unendlich, was sich im Grad von Zähler- und
Nennerpolynom widerspiegelt (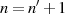 , vgl. Abschnitt 4.3).
, vgl. Abschnitt 4.3).
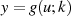 als auch
als auch 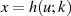 sind ungerade Funktionen, deshalb
sind ungerade Funktionen, deshalb 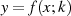 ebenfalls.
ebenfalls.Aus diesen Gründen kann man als rationale Transformationsfunktion
angeben.
Beweis. Die vorangegangenen Überlegungen erlauben es, als Ausgangspunkt für die Lösungsfunktion folgende Form anzugeben.
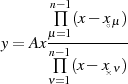
Nimmt man die konkreten Werte der Pole und Nullstellen hinzu
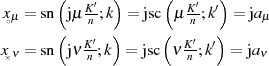
und berücksichtigt das betragsmäßig doppelte Auftreten aller Nullstellen und Pole,51 dann läßt sich die Ausgangsformel konkretisieren.
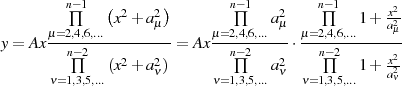
___
Eine weitere bekannte Form der Transformationsbeziehung 151 ist:52
 | (153) |
Beweis. Beide Darstellungen sind schnell zu beweisen, wenn man auf jeden Faktor im Zähler
bzw. Nenner von Gleichung 151 die Beziehung 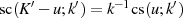 nach [AS72,
16.8] anwendet und danach geeignet umindiziert. Beispielhaft wird hier die beschriebene
Umformung für den Nenner durchgeführt, wobei der neue Index
nach [AS72,
16.8] anwendet und danach geeignet umindiziert. Beispielhaft wird hier die beschriebene
Umformung für den Nenner durchgeführt, wobei der neue Index 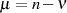 eingeführt wird.
eingeführt wird.
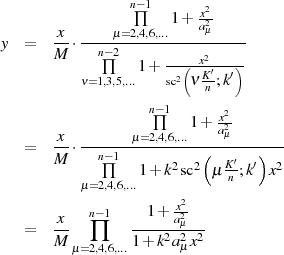
Die Nullstellen waren der Ausgangspunkt bei der Ermittlung der Koeffizienten von Nenner- und
Zählerpolynom in Transformationsbeziehung 151 bzw. 125. Sie liegen in diesem Fall nicht direkt auf
den schon desöfteren betrachteten Wegabschnitten 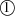 -
-  von
von  , sondern auf imaginären Punkten
innerhalb des Periodenrechtecks (vgl. auch Abbildung 18 sowie imaginäre Transformation nach
Gleichung 57, Abschnitt 57).
, sondern auf imaginären Punkten
innerhalb des Periodenrechtecks (vgl. auch Abbildung 18 sowie imaginäre Transformation nach
Gleichung 57, Abschnitt 57).
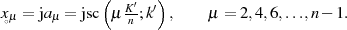
Die 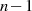 Pole wurden (wie die Nullstellen auch) schon bei der Herleitung der rationalen
Transformationsbeziehung bestimmt. Sie sind jedoch auch leicht aus Gleichung 151
abzulesen.53
Pole wurden (wie die Nullstellen auch) schon bei der Herleitung der rationalen
Transformationsbeziehung bestimmt. Sie sind jedoch auch leicht aus Gleichung 151
abzulesen.53
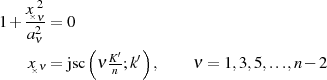
Die lokalen Extremwerte, welche auch in Abbildung 19 zu erkennen sind, liegen bei
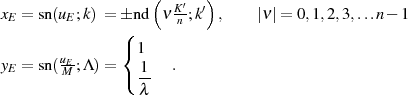

Einsetzen der Koeffizientenformel 152 in die rationale Transformationsbeziehung 153 führt zu den elliptischen Darstellungen

Die Formeln für den elliptischen Cosinus und die Delta-Amplitude kann man z. B. [Ach70, Tab. XXIII] entnehmen.
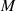
Der Multiplikator 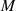 kann durch Evaluation der Transformationsgleichung 151 oder 153 an der Stelle
kann durch Evaluation der Transformationsgleichung 151 oder 153 an der Stelle
 gewonnen werden.
gewonnen werden.
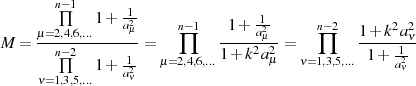 | (154) |
Einsetzen der Koeffizientenformel 152 führt zu einer weiteren, bekannten Darstellung des
Multiplikators 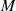 .
.
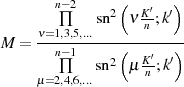 | (155) |
Beweis. Der Beweis ist nicht schwierig, wenn man 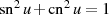 berücksichtigt.
berücksichtigt.
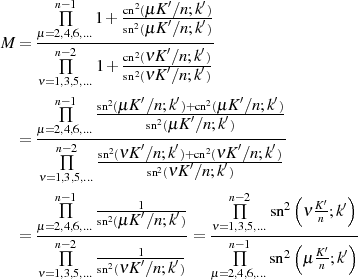
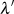
Das Modul  kann auf gleichem Wege wie der Multiplikator
kann auf gleichem Wege wie der Multiplikator 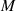 bestimmt werden, nur wird dazu der
schon bekannte Funktionswert
bestimmt werden, nur wird dazu der
schon bekannte Funktionswert  herangezogen, vgl. 18. Evaluation von
Transformationsbeziehung 151 an dieser Stelle ergibt sofort
herangezogen, vgl. 18. Evaluation von
Transformationsbeziehung 151 an dieser Stelle ergibt sofort
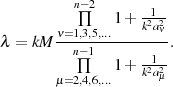
Wieder sind die Beziehungen 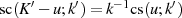 sowie
sowie 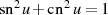 gefolgt von
Umindizierung im Zähler und Nenner günstig anwendbar, um ausführliche Darstellungen zu
entwickeln.
gefolgt von
Umindizierung im Zähler und Nenner günstig anwendbar, um ausführliche Darstellungen zu
entwickeln.
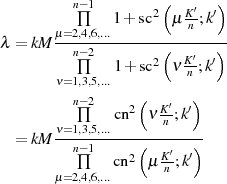
Ausgehend von der Transformationsfunktion nach Gleichung 153 kann eine weitere bekannte Formel
für 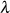 ermittelt werden. Sie bezieht Gleichung 154 für den Multiplikator
ermittelt werden. Sie bezieht Gleichung 154 für den Multiplikator 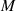 ein und stützt sich
(genauso wie bei der ersten elliptischen Haupttransformation, vgl. 136) auf die vierte Potenz der
Koeffizienten
ein und stützt sich
(genauso wie bei der ersten elliptischen Haupttransformation, vgl. 136) auf die vierte Potenz der
Koeffizienten  .
.