


Ein Bandpaßsystem hat typischerweise einen Durchlaßbereich, welcher sich von 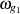 bis
bis 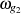 erstreckt (siehe Abbildung 3.3).
erstreckt (siehe Abbildung 3.3).
Aus dem Tiefpaß-Amplitudengang läßt sich eine solche Charakteristik ableiten, wenn man die Transformationsbeziehung (nach Tabelle 3.1)
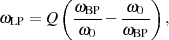 | (3.2) |
anwendet. Die Kreisfrequenz 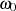 nimmt in diesem Fall die Bedeutung einer Mittenfrequenz an,
nimmt in diesem Fall die Bedeutung einer Mittenfrequenz an, 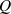 bezeichnet man als Güte. Die Interpretation von
bezeichnet man als Güte. Die Interpretation von 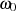 wird einsichtig, wenn man Gleichung 3.2
folgendermaßen umformt (vgl. auch [Pap62, 7-1]):
wird einsichtig, wenn man Gleichung 3.2
folgendermaßen umformt (vgl. auch [Pap62, 7-1]):
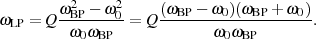
Um auch für die Güte 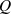 eine anschauliche Aussage zu erhalten, wenden wir (nach Vereinfachung für
eine anschauliche Aussage zu erhalten, wenden wir (nach Vereinfachung für
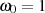 ) auf
) auf
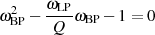
die quadratische Lösungsformel (vorerst formal) an:
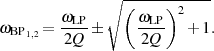 | (3.3) |
An Hand der mehr anschaulichen Umformung
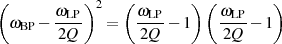
wird deutlich, daß 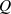 insbesondere auf die Skalierung der Tiefpaßfrequenz
insbesondere auf die Skalierung der Tiefpaßfrequenz 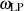 und in Folge auf die
Breite des Durchlaßbereichs wirkt.
und in Folge auf die
Breite des Durchlaßbereichs wirkt.
Was wir bezüglich Formel 3.3 noch berücksichtigen müssen ist die Tatsache, daß sich Frequenztransformationen sowohl auf positive als auch negative Kreisfrequenzen beziehen. Hinzu kommt, daß wegen
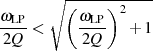
eine der beiden Frequenzen 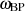 in der gewonnenen Lösungsformel immer negativ wird. Man darf
sich nun insofern nicht täuschen lassen, als das die andere zugehörige Frequenz (mit gleichem
Vorzeichen) durch Einsetzen von
in der gewonnenen Lösungsformel immer negativ wird. Man darf
sich nun insofern nicht täuschen lassen, als das die andere zugehörige Frequenz (mit gleichem
Vorzeichen) durch Einsetzen von 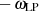 erzeugt wird. Für den (normierten) Zusammenhang zwischen
erzeugt wird. Für den (normierten) Zusammenhang zwischen
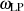 und
und 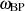 ergibt sich aus diesem Grund letztlich:
ergibt sich aus diesem Grund letztlich:
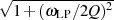 liegen. Für die Abbildung der
Grenzfrequenz
liegen. Für die Abbildung der
Grenzfrequenz 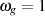 der normierten Approximationsfunktion bedeutet dies:
der normierten Approximationsfunktion bedeutet dies:
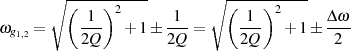
und deshalb für die geometrische Mittenfrequenz des Bandpaß’:4
Den Sinn,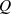 als Gütedefinition herzunehmen, unterstreicht folgende Formel für die absolute
Bandbreite (bei Mittenfrequenz
als Gütedefinition herzunehmen, unterstreicht folgende Formel für die absolute
Bandbreite (bei Mittenfrequenz 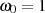 ):
):
Was die Transformation der Pol- und Nullstellen angeht, so gilt dafür ebenfalls Formel 3.4. Um eine gewisse Geradlinigkeit zu wahren, wählen wir jedoch den “umständlichen” Weg5 und substituieren in der Produktdarstellung
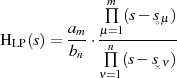
zuerst die 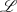 -Variable zu
-Variable zu 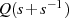 .
.
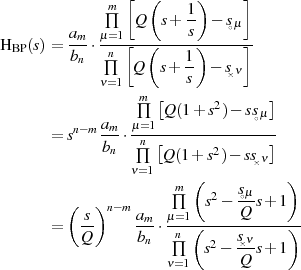
Aus jedem Linearfaktor der Tiefpaß-Übertragungsfunktion entspringen (wegen des quadratischen
Auftretens von  in letzter Gleichung) also zwei neue Wurzeln. Die Evaluation erfolgt durch
Nullsetzen eines Faktors (hier beispielhaft an einer Nullstelle) und Anwendung der quadratischen
Lösungsformel.
in letzter Gleichung) also zwei neue Wurzeln. Die Evaluation erfolgt durch
Nullsetzen eines Faktors (hier beispielhaft an einer Nullstelle) und Anwendung der quadratischen
Lösungsformel.
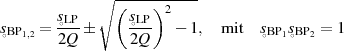
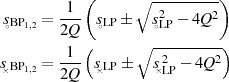
wieder zwei neue Nullstellen hervorbringt, wobei reelle Nullstellen nur unter der
Bedingung 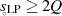 auch wieder reelle erzeugen (ansonsten ein konjugiert-komplexes
Nullstellenpaar);
auch wieder reelle erzeugen (ansonsten ein konjugiert-komplexes
Nullstellenpaar);
 ein Bandpaß vom Grad
ein Bandpaß vom Grad  wird (siehe voriger Punkt);
wird (siehe voriger Punkt);
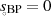 mit der Vielfachheit
mit der Vielfachheit  führt;
führt;
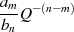
wirkt.