


Der BESSEL- bzw. THOMSON-Tiefpaß ist vom Syntheseansatz her kein System mit dem Ziel der
Selektion von Frequenzanteilen (wie die vorangegangen Filter), sondern eher als verzerrungsarmes
Übertragungssystem zu verstehen. Approximiert wird dabei die Übertragungsfunktion 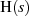 eines
idealen LTI-Systems bzw. dessen linearen Phasengang [Tho49, Sto51].
eines
idealen LTI-Systems bzw. dessen linearen Phasengang [Tho49, Sto51].
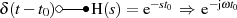
Die Verzögerungszeit 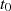 ignorierend konzentrieren wir uns zuerst auf die Darstellungsmöglichkeiten
der Exponentialfunktion
ignorierend konzentrieren wir uns zuerst auf die Darstellungsmöglichkeiten
der Exponentialfunktion 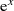 durch Hyperbelfunktionen
durch Hyperbelfunktionen
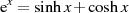
und deren Reihenentwicklungen.
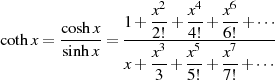
Bricht man die Reihen für 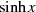 und
und 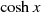 nun einfach nach einer beschränkten Anzahl von
Gliedern ab, dann
nun einfach nach einer beschränkten Anzahl von
Gliedern ab, dann
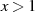 ,
unbefriedigend
,
unbefriedigend
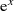 unter Umständen kein HURWITZ-Polynom24
(als Bedingung für stabile Systeme) sein.
unter Umständen kein HURWITZ-Polynom24
(als Bedingung für stabile Systeme) sein.Besser ist an dieser Stelle eine Kettenbruchentwicklung – mit den vorteilhaften Eigenschaften:
Durch eigene Rechnung oder Verwendung eines geeigneten Nachschlagewerks erhält man aus der Reihenentwicklung den folgenden Kettenbruch des hyperbolischen Cotangens:
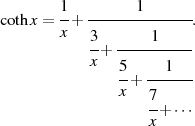 | (2.30) |
Bricht man diese Entwicklung nach  Schritten ab, so kann man daraus eine rationalen Bruch
Schritten ab, so kann man daraus eine rationalen Bruch
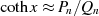 bestimmen. Durch vollständige Induktion kann verifiziert werden, daß Zähler und
Nenner den Rekursionsformeln
bestimmen. Durch vollständige Induktion kann verifiziert werden, daß Zähler und
Nenner den Rekursionsformeln

gehorchen.25
Berücksichtigt man die Anfangswerte 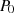 ,
, 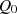 ,
, 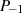 und
und 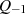 , dann lassen die Formeln sofort
erkennen, daß das Zählerpolynom
, dann lassen die Formeln sofort
erkennen, daß das Zählerpolynom 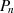 nur gerade Potenzen von
nur gerade Potenzen von  enthält, das Nennerpolynom
enthält, das Nennerpolynom 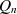 dagegen alle Ungeraden.
dagegen alle Ungeraden.
Kommen wir nun zurück zur Approximation von 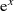 und interpretieren
und interpretieren 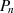 und
und 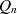 als Näherung für
Zähler und Nenner in
als Näherung für
Zähler und Nenner in
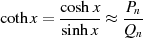
und in Konsequenz als Summenterme in der Exponentialfunktion
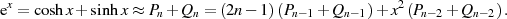
Die Summe (und gleichzeitig Berechnungsvorschrift auf der rechten Seite) nennt man BESSEL-Polynom
vom Grad  .
.
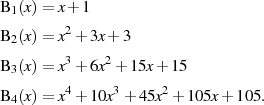
Mit der so gewonnen Näherung für 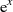 kann man als Übertragungsfunktion des verzerrungsarmen
Systems
kann man als Übertragungsfunktion des verzerrungsarmen
Systems
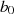 nur zum Zwecke der Normierung auf
nur zum Zwecke der Normierung auf 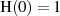 hinzugefügt wurde. Da in
der Kettenbruchentwicklung des Quotienten
hinzugefügt wurde. Da in
der Kettenbruchentwicklung des Quotienten 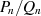 nach Formel 2.30 alle linksseitigen
Summanden
nach Formel 2.30 alle linksseitigen
Summanden 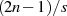 positive Koeffizienten (
positive Koeffizienten (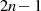 ) haben, handelt es sich bei
) haben, handelt es sich bei
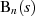 wirklich um ein HURWITZ-Polynom [Cau54, VIII-15b], [Fri79b, 3.1.3], [Che95,
44.5].26
wirklich um ein HURWITZ-Polynom [Cau54, VIII-15b], [Fri79b, 3.1.3], [Che95,
44.5].26
Einen typischen Frequenzgang nach Gleichung 2.32 zeigt Abbildung 2.8. Recht gut zu erkennen ist dabei der relativ lineare Phasengang, welcher sich im Nullpunkt als maximal flache Gruppen- bzw. Signallaufzeit präsentiert.