Wirkung im Zeitbereich

1.1 Wirkung im Zeitbereich

Mit Hilfe des Quadraturmodulators lassen sich quasi alle modernen (Trägerfrequenz-) Modulationsverfahren realisieren. Betrachten wir dazu sein Blockbild nach Abbildung 1.

Abbildung 1:

Quadraturmodulator

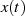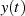Er besitzt zwei Eingänge I (in-phase) und Q (quadrature-phase) mit den zugeordneten Zeitsignale $x(t)$ und $y(t)$ , welche mit Hilfe eines Trägers (der Kreisfrequenz 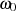$ω0$ ) zu einem Modulationsprodukt 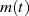$m(t)$ verknüpft werden.¹

m(t)= x(t)cos(ω0t)− y(t)sin(ω0t)

(1)

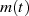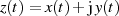Man kann das Modulationsprodukt $m(t)$ nach Formel 1 auch als Realteil des Produktes zweier Zeiger in der komplexen Ebene beschreiben. Dazu sei die komplexe Größe $z(t) = x(t)+ jy(t)$ definiert und dann folgendermaßen verwendet:

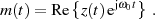{ jωt} m(t)= Re z(t)e 0 .

(2)

Das In-Phase Signal 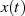$x(t)$ stellt also den Realteil von 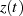$z(t)$ , das Quadrature-Phase Signal den Imaginärteil 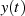$y(t)$ .²