


Holomorphe bzw. analytische Funktionen2 sind solche, deren Grenzwert
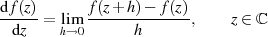 | (1) |
existiert und eindeutig ist, die also an der Stelle  differenzierbar sind. Man fordert hierbei nicht unbedingt,
daß
differenzierbar sind. Man fordert hierbei nicht unbedingt,
daß 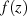 für alle
für alle  einen solchen Grenzwert hat – man kann sich auch auf ein bestimmtes Gebiet
beschränken.3
Die “Einwertigkeit” des Grenzwertes (One-Valued) spielt auf Funktionen an, bei denen er davon
abhängt, aus welcher Richtung man sich nähert. Er kann sogar dann existieren, wenn der Funktionswert
selbst nicht existiert (wie z. B.
einen solchen Grenzwert hat – man kann sich auch auf ein bestimmtes Gebiet
beschränken.3
Die “Einwertigkeit” des Grenzwertes (One-Valued) spielt auf Funktionen an, bei denen er davon
abhängt, aus welcher Richtung man sich nähert. Er kann sogar dann existieren, wenn der Funktionswert
selbst nicht existiert (wie z. B. 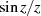 an der Stelle
an der Stelle 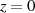 ). Nicht analytisch sind unter anderen die
Funktionen
). Nicht analytisch sind unter anderen die
Funktionen 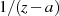 bei
bei  oder auch
oder auch 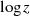 für
für 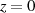 .
.
Eine Schlußfolgerung von B. RIEMANN in Bezug auf die “Einwertigkeit” des Differentialquotienten
(nach Gleichung 1) der analytischen Funktion 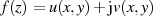 mit
mit 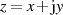 war, daß bei Annäherung in
war, daß bei Annäherung in  -Richtung, also bei konstantem
-Richtung, also bei konstantem 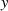 (horizontal) der gleiche
Grenzwert gelten muß, wie bei Annäherung aus
(horizontal) der gleiche
Grenzwert gelten muß, wie bei Annäherung aus 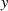 -Richtung (bei konstantem
-Richtung (bei konstantem  , also
vertikal).4
, also
vertikal).4
Vergleich von Real- und Imaginärteil liefert die CAUCHY-RIEMANN’schen Differentialgleichungen5
und wegen der Unabhängigkeit des Grenzwertes von jedweder Annäherungsrichtung
(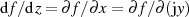 ) außerdem
) außerdem
bzw.