


Die spezielle konforme Abbildung 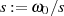 nach Tabelle 3.1
(Inversion3 )
entspricht im Amplitudengang einer Spiegelung um die Frequenz
nach Tabelle 3.1
(Inversion3 )
entspricht im Amplitudengang einer Spiegelung um die Frequenz 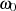 , wenn man von einer
logarithmischen Frequenzachse ausgeht (siehe auch Abbildung 3.2).
, wenn man von einer
logarithmischen Frequenzachse ausgeht (siehe auch Abbildung 3.2).
Da bei den Standardapproximationen die normierte Grenzfrequenz üblicherweise zu 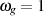 gewählt wird, kann man
gewählt wird, kann man 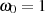 setzen und für die Übertragungsfunktion in der
setzen und für die Übertragungsfunktion in der  -Ebene
schreiben:
-Ebene
schreiben:
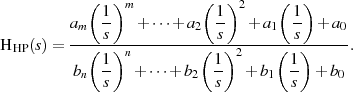
Multipliziert man noch den Nenner mit 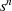 und den Zähler mit
und den Zähler mit 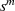 , so führt dies zu einer Umordnung
der Koeffizienten.
, so führt dies zu einer Umordnung
der Koeffizienten.
Die Wirkung der Transformation auf die rationale Übertragungsfunktion nach Formel 3.1
korrespondiert mit einer bestimmten Verschiebung der Pol- und Nullstellen in der komplexen Ebene.
Sehen wir uns dazu die Übertragungsfunktion 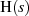 eines Tiefpaß’ in Linearfaktordarstellung
an.
eines Tiefpaß’ in Linearfaktordarstellung
an.
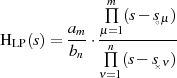
Einsetzen der Substitution  läßt daraus
läßt daraus

werden, d. h. :