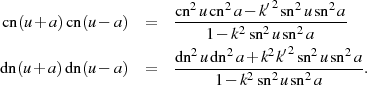Die Additionstheoreme der elliptischen Funktionen haben grundlegende Bedeutung für viele weitere Formeln.
Deshalb haben zahlreiche Mathematiker des 18. und 19. Jahrhunderts, unter anderem A.-M. LEGENDRE,
C.G.J. JACOBI, J. LANDEN und C.F. GAUSS, sich mit dem Beweis dieser Gleichungen
beschäftigt.12
Zuerst hat jedoch L. EULER im Jahre 1756/57 das Additionstheorem des elliptischen Sinus’
(EULER-Theorem) bewiesen [WW27, §  ], [Hur00, II-3].
], [Hur00, II-3].
Beweis. Der hier dargelegte Beweis folgt (wie auch [Ach70, § 28]) in wesentlichen
Schritten den Ausführungen von J.G. DARBOUX. Als Ausgangspunkt dient dabei die
Differentialgleichung der Transformationstheorie (Formel 69 für den Fall 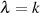 und
und 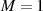 ),
),

für die hier eine Lösung gefunden werden soll. Genauso wie in Abschnitt 4.5 erweist es sich als günstig zur Parameterform des Differentials überzugehen.
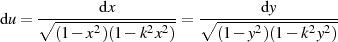 | (41) |
Die einzelnen Ableitungen nach  kann man integrieren
kann man integrieren
und (bei Berücksichtigung der Integrationskonstante  ) Gleichung 41 auch darstellen
als:
) Gleichung 41 auch darstellen
als:
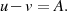
Nach diesen einfachen Vorbetrachtungen differenziert man nun das Quadrat der Ableitungen 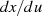 sowie
sowie 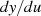 in den Gleichungen 42 nocheinmal nach
in den Gleichungen 42 nocheinmal nach  , also folgendermaßen:
, also folgendermaßen:
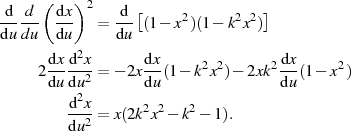
Auf dem gleichen Weg gelangt man zu:
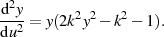
Stellt man die zuletzt gewonnenen Formeln nach 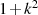 um und setzt sie nach Multiplikation mit
um und setzt sie nach Multiplikation mit  beide gleich, so erhält man das folgende wichtige Zwischenergebnis
beide gleich, so erhält man das folgende wichtige Zwischenergebnis
Jetzt soll unabhängig davon der Ausdruck
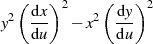
bestimmt werden. Einsetzen der Ableitungen von 42 gefolgt von Ausmultiplizieren und Zusammenfassen führt zur nächsten Zwischengleichung.
Nun dividiert man Gleichung 43 durch die soeben entwickelte und wendet auf den linken Nenner den binomischen Satz an.
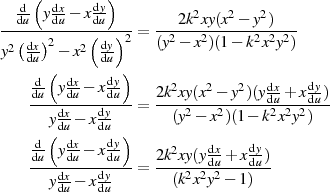
Es ist zu erkennen, daß auf beiden Seiten Zähler und Nenner dem logarithmischen Differentiationssatz ![[lnf(u)]′ = f ′(u)∕f(u)](elliptic235x.png) entsprechen.13
entsprechen.13

Integration nach  und Einsetzen der Differentiale von Gleichung 42 führt zu
und Einsetzen der Differentiale von Gleichung 42 führt zu
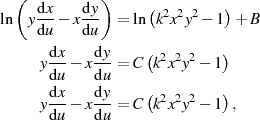
also
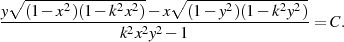
Mit  und
und 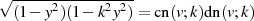 nach
Definitionsgleichung 32 und 30 gilt also:
nach
Definitionsgleichung 32 und 30 gilt also:

Die Konstante 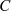 muß nun aber eine Funktion von
muß nun aber eine Funktion von 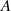 sein, also
sein, also 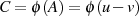 gelten. Um die
Form von
gelten. Um die
Form von 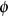 zu finden kann man z. B.
zu finden kann man z. B. 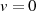 setzen, was zu
setzen, was zu 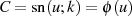 führt. Also ist die
Form von
führt. Also ist die
Form von 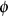 der elliptische Sinus und somit ist der Beweis auf der Grundlage des folgenden
Subtraktionstheorems erbracht.
der elliptische Sinus und somit ist der Beweis auf der Grundlage des folgenden
Subtraktionstheorems erbracht.
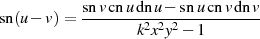
__
Die beiden anderen elliptischen Basisfunktionen sind entweder genauso oder aber aus ihren
Definitionsgleichungen abzuleiten. Hier wird jedoch darauf verzichtet und statt dessen nur das Ergebnis
präsentiert (wobei in den Formeln wieder auf das Modul 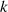 verzichtet wird).
verzichtet wird).
Äußerst interessant sind auch die daraus abgeleiteten Relationen14 für den elliptischen Sinus
die insbesondere in der Transformationstheorie häufig auch in folgender Form anzutreffen sind (mit
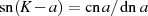 , vgl. Tabelle 3)
, vgl. Tabelle 3)
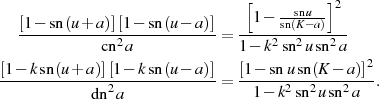
Im Zusammenhang mit den quadratischen Transformationen ist auch folgende Relation interessant
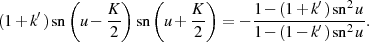 | (50) |
Beweis. Es handelt sich hier um einen Spezialfall von Formel 47 mit 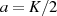 .
.
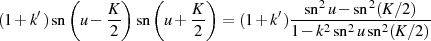
Ersetzt man noch den speziellen Wert 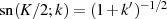 , so ist der Beweis schon
erbracht.
, so ist der Beweis schon
erbracht.
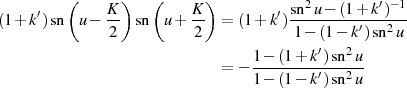
Weitere ausgewählte Formeln für  und
und 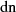 sind:
sind: