


Wendet man die GAUSS-Transformation entsprechend Gleichung 113 zur Berechnung von
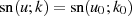 in der Form
in der Form
an (vgl. [Bul65], [HR63]), so führt dies für 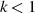 letztlich zu einem
Modul
letztlich zu einem
Modul 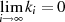 . Bricht man den Vorgang nach
. Bricht man den Vorgang nach 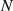 Iterationen ab, so
gilt:59
Iterationen ab, so
gilt:59
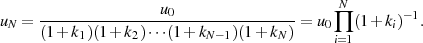
Mit 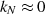 kann man für
kann man für 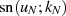 nun folgendermaßen
nähern:60
nun folgendermaßen
nähern:60
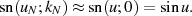
Nach Ermittlung von 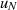 kann man durch inverse Interpretation (
kann man durch inverse Interpretation (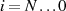 ) der Abstiegsgleichung 174
rückwärts
) der Abstiegsgleichung 174
rückwärts 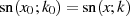 berechnen.
berechnen.
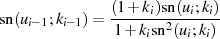
Das Modul 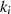 kann hierfür äquivalent zu Formel 102 in jedem Schritt rückwärts berechnet
werden.61
kann hierfür äquivalent zu Formel 102 in jedem Schritt rückwärts berechnet
werden.61
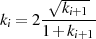
Nach [Pev92] ist der absolute Gesamtfehler des Verfahrens kleiner als 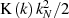 .
.