


Das Vollständige Elliptische Integral 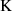 kann ausgehend von Gleichung 168 ebenfalls mit Hilfe des
AGM-Algorithmus’ berechnet werden. Dazu wird Gleichung 168 als vollständiges elliptisches Integral
erster Art
kann ausgehend von Gleichung 168 ebenfalls mit Hilfe des
AGM-Algorithmus’ berechnet werden. Dazu wird Gleichung 168 als vollständiges elliptisches Integral
erster Art 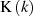 ausgedrückt, indem man wieder Formel 28 hinzuzieht.
ausgedrückt, indem man wieder Formel 28 hinzuzieht.
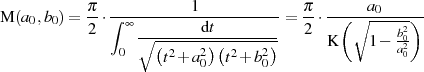 | (169) |
Umstellen nach 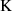 bedeutet:
bedeutet:
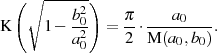
Wählt man nun z. B. 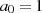 , was die Voraussetzung
, was die Voraussetzung 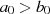 erfüllt und setzt
erfüllt und setzt 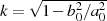 als
Argument, so gilt für
als
Argument, so gilt für 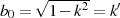 . Damit berechnet sich das Elliptische Integral erster Art zu:
. Damit berechnet sich das Elliptische Integral erster Art zu:
was der zugehörige Algorithmus 1 wiederspiegelt.
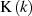 mittels AGM
mittels AGMFür die Darstellung von 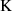 mit Hilfe des Modulwinkels
mit Hilfe des Modulwinkels 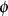 , d. h. für
, d. h. für 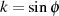 , ist
, ist 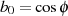 zu
wählen.
zu
wählen.
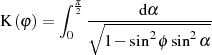
Jetzt soll noch kurz auf die Produktdarstellung für 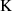 eingegangen werden. Dazu benutzen wir
Formel 94 aus Abschnitt 4.7.1 im Sinne von
eingegangen werden. Dazu benutzen wir
Formel 94 aus Abschnitt 4.7.1 im Sinne von 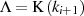 ,
, 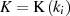 und schreiben als reelle
(Viertel-) Periodenbeziehung
und schreiben als reelle
(Viertel-) Periodenbeziehung
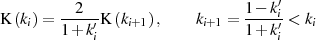
mit dem Ausgangspunkt 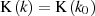 . Bei einer unendlichen Anzahl von Iterationen wird
. Bei einer unendlichen Anzahl von Iterationen wird 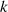 Null
und wegen Gleichung 26 gilt:
Null
und wegen Gleichung 26 gilt:
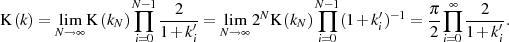
Das heißt, die Zwischenwerte 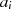 und
und 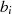 eines normalen AGM könnten zur Berechnung des Produkts
verwendet werden, wenn man die Beziehung
eines normalen AGM könnten zur Berechnung des Produkts
verwendet werden, wenn man die Beziehung 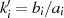 berücksichtigt.
berücksichtigt.