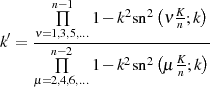Für gerades 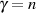 muß die Integrationskonstante
muß die Integrationskonstante 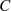 aus Abschnitt 4.5 die reelle Viertelperiode
aus Abschnitt 4.5 die reelle Viertelperiode
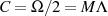 annehmen (vgl. auch Tabelle 6),
annehmen (vgl. auch Tabelle 6),
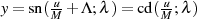 | (139) |
damit 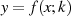 eine gerade Funktion und außerdem auf Wegabschnitt
eine gerade Funktion und außerdem auf Wegabschnitt  in Abbildung 8a reell
ist. Der zugeordnete Verlauf des Parameters
in Abbildung 8a reell
ist. Der zugeordnete Verlauf des Parameters  (inklusive der positiven Nullstellen und Pole) ist dazu
nocheinmal anschaulich in Abbildung 16 illustriert.
(inklusive der positiven Nullstellen und Pole) ist dazu
nocheinmal anschaulich in Abbildung 16 illustriert.
Der Funktionsverlauf von 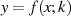 entspricht prinzipiell dem für ungerade
entspricht prinzipiell dem für ungerade  , nur der
Funktionswert an der Stelle
, nur der
Funktionswert an der Stelle 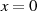 ist wegen der Verschiebung entlang der reellen Achse
ist wegen der Verschiebung entlang der reellen Achse 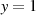 (siehe
Abbildung 17).
(siehe
Abbildung 17).
Aus den wichtigsten Eigenschaften der Differentialgleichung 70 sowie der Transformationsfunktion, welche in Abschnitt 4.5 erarbeitet wurden, kann man wiederum auf die Form der (diesmal geraden) rationalen Transformationsfunktion schließen [Ach70, Tab. XXII].
Sie erfüllt unter anderem auch die speziellen Werte 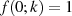 und
und 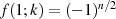 .
Aus dem Funktionswert
.
Aus dem Funktionswert 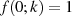 ergibt sich die noch erwähnenswerte
Beziehung:49
ergibt sich die noch erwähnenswerte
Beziehung:49
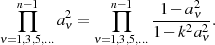
Wie schon Abbildung 16 anschaulich zeigt, ist die Lage der Pole und Nullstellen (gegenüber
ungeradem Grad  ) entsprechend der Integrationskonstante
) entsprechend der Integrationskonstante 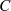 um
um 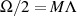 , also für
, also für  um
um 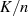 verschoben (vgl. Wegabschnitte
verschoben (vgl. Wegabschnitte  und
und  ).
).
Gleiches gilt auch für die Extremwerte
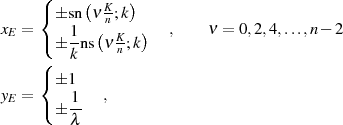
wobei einer der Werte für 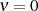 bei
bei  zu liegen kommt.
zu liegen kommt.
Transformationsbeziehung für 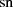 Die Transformationsbeziehung für den elliptischen Sinus ist wieder direkt in Gleichung 140
enthalten, wenn man
Die Transformationsbeziehung für den elliptischen Sinus ist wieder direkt in Gleichung 140
enthalten, wenn man  und
und 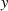 durch die entsprechenden elliptischen Funktionen ersetzt.
durch die entsprechenden elliptischen Funktionen ersetzt.
Eine weitere interessante Darstellung der Transformationsbeziehung 129 ergibt sich auch hier mit Hilfe von Multiplikationsformel 47.
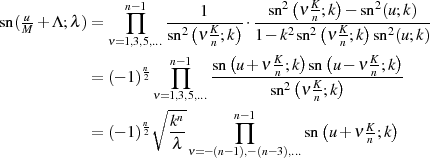
Transformationsbeziehung für  Ähnlich wie für den Fall eines ungeraden
Ähnlich wie für den Fall eines ungeraden  (vgl. Abschnitt 4.8.7) kann man auch hier vorgehen und
erhält in Folge
(vgl. Abschnitt 4.8.7) kann man auch hier vorgehen und
erhält in Folge
Beweis. Auch diesmal kann man die Gleichung für  durch Betrachtung der Pole und
Nullstellen herleiten (vgl. Abschnitt 4.8.7). Dazu geht man wieder von einem Ansatz aus, in
welchem eigentlich nur ein Vorfaktor zu bestimmen ist.
durch Betrachtung der Pole und
Nullstellen herleiten (vgl. Abschnitt 4.8.7). Dazu geht man wieder von einem Ansatz aus, in
welchem eigentlich nur ein Vorfaktor zu bestimmen ist.
![4n−2 ( )
∏ x − sn μKn-;k
1− y2 = cn2( u+ Λ; λ)= A2 ---μ=0,2,4,...----------------
M n−1 [ 2 2( K- ) 2]2
ν=∏1,3,5,... 1− k sn νn;k x](elliptic1110x.png)
Wegen der Symmetrie des elliptischen Sinus um 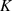 , d. h.
, d. h. 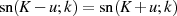 sowie
der Spiegelungsbeziehung
sowie
der Spiegelungsbeziehung 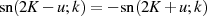 kann vorher noch das Produkt im
Zähler reduziert werden. Löst man dabei außerdem die Faktoren für
kann vorher noch das Produkt im
Zähler reduziert werden. Löst man dabei außerdem die Faktoren für 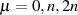 und
und 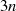 heraus, so ergibt sich
heraus, so ergibt sich
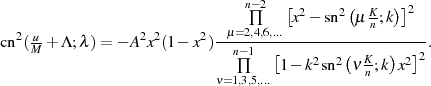
Um den Vorfaktor 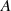 nun zu bestimmen, kann man z. B. den Funktionswert für
nun zu bestimmen, kann man z. B. den Funktionswert für  heranziehen,
welcher schon zu
heranziehen,
welcher schon zu 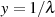 ermittelt wurde.
ermittelt wurde.
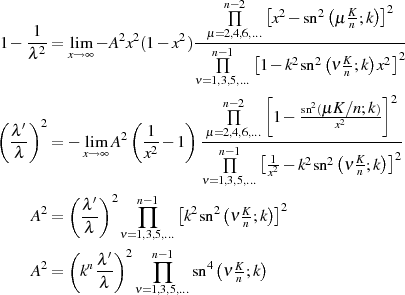
Einsetzen des gerade ermittelten Vorfaktors führt zu einer ersten geschlossen Lösung
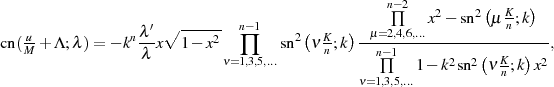
welche allerdings nicht gerade übersichtlich ist. Mit Vorgriff auf die Berechnungsformeln für 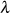 und
und
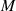 (Gleichungen 146 und 147) und deren Beziehung zueinander
(Gleichungen 146 und 147) und deren Beziehung zueinander
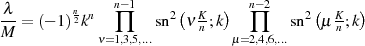
ist man in der Lage, eine etwas kürzere Form anzugeben.
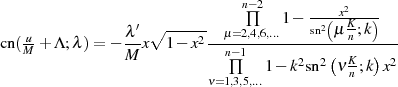
__
Transformationsbeziehung für 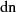 Die entsprechende Beziehung für
Die entsprechende Beziehung für 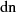 lautet:
lautet:
Beweis. Auch hier geht man am besten wieder von den Nullstellen aus, welche entsprechend
der Definition für die elliptische Delta-Amplitude dort liegen müssen, wo 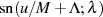 den
Wert
den
Wert 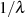 annimmt. Genau diese Stellen haben wir aber schon als Extremwerte des
Funktionsverlaufes dieser Transformation erkannt. Sie liegen bei
annimmt. Genau diese Stellen haben wir aber schon als Extremwerte des
Funktionsverlaufes dieser Transformation erkannt. Sie liegen bei 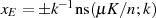 mit
mit
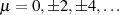 , was folgenden Ansatz für eine Linearfaktordarstellung rechtfertigt
, was folgenden Ansatz für eine Linearfaktordarstellung rechtfertigt
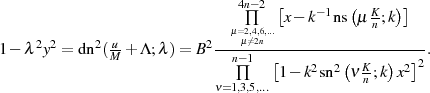
Wieder berücksichtigen wir, daß 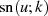 eine ungerade Funktion mit der Halbperiode
eine ungerade Funktion mit der Halbperiode
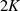 ist und extrahieren außerdem den speziellen Wert
ist und extrahieren außerdem den speziellen Wert 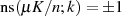 für die Indizes
für die Indizes
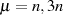 .
.
![n− 2 [ ( )]2
∏ x2− k−2ns2 μKn-;k
dn2( u-+ Λ;λ) = B2(x2− k−2)μ=2,4,6,...------------------
M n− 1 [ 2 2( K- ) 2]2
ν=∏1,3,5,... 1− k sn νn;k x](elliptic1138x.png)
Der Vorfaktor kann z. B. durch Einsetzen des Funktionswertes an der Stelle 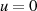 , d. h.
, d. h.
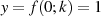 bestimmt werden.
bestimmt werden.
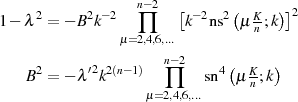
Mit diesem Ausdruck für 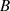 kann man nun die Transformationsbeziehung für
kann man nun die Transformationsbeziehung für 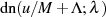 konkretisieren.
konkretisieren.
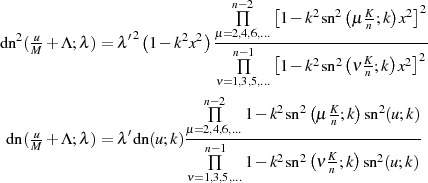
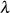
Das Modul 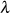 kann auf den verschiedensten Wegen bestimmt werden, z. B. auch wieder aus der
Eigenschaft der Invarianz von Differentialgleichung 69 für
kann auf den verschiedensten Wegen bestimmt werden, z. B. auch wieder aus der
Eigenschaft der Invarianz von Differentialgleichung 69 für 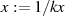 und
und 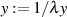 nach
Formel 81.
nach
Formel 81.
Beweis. An dieser Stelle soll zur Abwechslung ein anderer, ebenfalls sehr einfacher Weg,
beschritten werden. Dazu evaluiert man Transformationsbeziehung 140 am Extremwert
 , wo bekanntlich
, wo bekanntlich 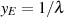 gelten muß.
gelten muß.
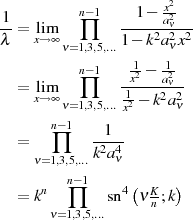
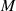
Der Multiplikator 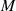 hat im Fall eines geraden
hat im Fall eines geraden  den Wert
den Wert
Beweis. Der Multiplikator 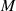 kann diesmal nicht durch einfaches Einsetzen spezieller Werte
ermittelt werden, da er in der rationalen Form 140 nicht auftaucht. Statt dessen wird hier die
erste Ableitung der elliptischen als auch der rationalen Transformationsbeziehung herangezogen
und mit deren Hilfe
kann diesmal nicht durch einfaches Einsetzen spezieller Werte
ermittelt werden, da er in der rationalen Form 140 nicht auftaucht. Statt dessen wird hier die
erste Ableitung der elliptischen als auch der rationalen Transformationsbeziehung herangezogen
und mit deren Hilfe 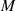 bestimmt. Zuerst wenden wir uns deshalb dem Ausgangsproblem
der Transformationstheorie, nämlich Differentialgleichung 71 zu. Um einen relativ einfachen
Lösungsweg zu beschreiten, konzentrieren wir uns dabei auf die Nullstellen
bestimmt. Zuerst wenden wir uns deshalb dem Ausgangsproblem
der Transformationstheorie, nämlich Differentialgleichung 71 zu. Um einen relativ einfachen
Lösungsweg zu beschreiten, konzentrieren wir uns dabei auf die Nullstellen 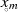 bzw.
bzw. 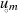 mit
mit
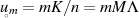 (
( ungerade).
ungerade).
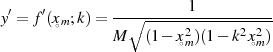
Aus dieser Gleichung kann man, wenn 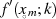 bekannt ist, sofort den Parameter
bekannt ist, sofort den Parameter 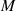 ermitteln.
ermitteln.
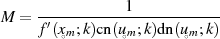 | (148) |
Die erste Ableitung der rationalen Transformationsbeziehung 140 kann durch logarithmische Differentiation gewonnen werden. Dazu seien vorab noch die folgenden Kurzformen vereinbart und ihre Ableitungen gebildet.

Es folgt die eigentliche Differentiation von
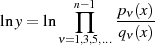
zu
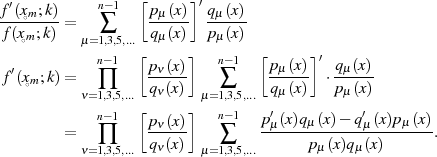
Setzt man jetzt die Nullstelle 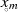 ein, dann verschwindet
ein, dann verschwindet 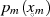 und demzufolge (eigentlich) das
ganze Produkt
und demzufolge (eigentlich) das
ganze Produkt 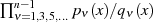 . Da in diesem Fall aber der Summenterm mit
. Da in diesem Fall aber der Summenterm mit 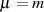 eine behebbare Unbestimmtheit aufweist (Kürzen von
eine behebbare Unbestimmtheit aufweist (Kürzen von 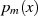 im Produkt mit
im Produkt mit 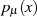 im
Nenner der Summe), verschwindet der Summenausdruck. Dabei gilt es
im
Nenner der Summe), verschwindet der Summenausdruck. Dabei gilt es 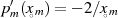 zu
berücksichtigen.
zu
berücksichtigen.

Durch Hinzunahme von Multiplikationsformel 47, kann man (ähnlich wie bei der Transformationsbeziehung) weiter vereinfachen zu:
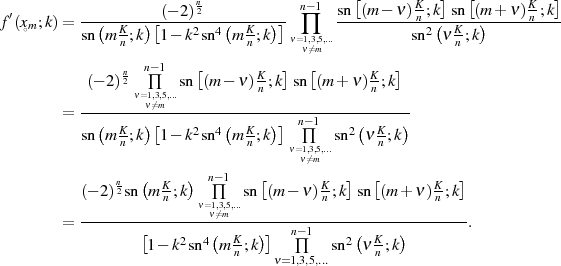
Die Indizes  bzw.
bzw.  durchlaufen, wenn man sie zusammenfaßt, alle geraden
Werte von
durchlaufen, wenn man sie zusammenfaßt, alle geraden
Werte von 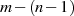 bis
bis 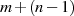 , ausgenommen die Werte
, ausgenommen die Werte 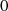 und
und 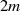 , für die
, für die
 gilt. Mit etwas Vorstellungskraft für den Verlauf des elliptischen Sinus und den
daraus generierten Nullstellen und Extremwerten ist offensichtlich, daß (abgesehen von den
zwei genannten) alle Werte
gilt. Mit etwas Vorstellungskraft für den Verlauf des elliptischen Sinus und den
daraus generierten Nullstellen und Extremwerten ist offensichtlich, daß (abgesehen von den
zwei genannten) alle Werte 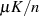 (für gerades
(für gerades 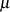 ) einer Halbperiode des elliptischen
Sinus’ durchlaufen werden. Der Produktterm im Zähler ist demzufolge auch darstellbar
als
) einer Halbperiode des elliptischen
Sinus’ durchlaufen werden. Der Produktterm im Zähler ist demzufolge auch darstellbar
als
![[ ]2
n−2 ( K- )
n−1 [ ] [ ] μ=∏2,4,...sn μn ;k
∏ sn (m − ν)K-;k sn (m + ν)K-;k = -------(-----)-----.
ν=1,3,5,... n n sn 2m Kn-;k
ν⁄=m](elliptic1188x.png)
Der Ausdruck im Nenner dieser Gleichung kann durch Anwendung der Verdoppelungsformel 51 so angepaßt werden
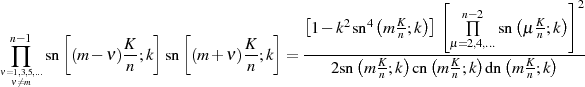
daß die Ableitung an einer Nullstelle nun geschlossen dargestellt werden kann.
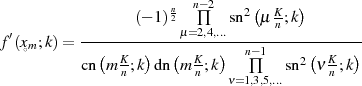 | (149) |
Einsetzen in Berechnungsformel 148 liefert (endlich) den Multiplikator 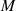 .
.
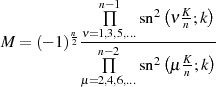
_
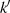
Die Formel für das komplementäre Modul 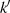 kann durch Evaluation der Beziehung 145 für
kann durch Evaluation der Beziehung 145 für 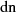 an
der Stelle
an
der Stelle 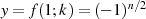 ermittelt werden.
ermittelt werden.