Imaginare Argumente

3.10 Imaginäre Argumente

Ausgehend von den grundlegenden Definitionsgleichungen des elliptischen Sinus’

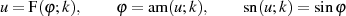
sowie den Beziehungen 18 und 19 zur imaginären Transformation des elliptischen Integrals 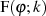$F(φ;k)$ kann man für ein imaginäres Argument 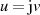$u= jv$ schreiben:

[ ] u= F (φ; k)= F(jξ ;k)= jF arctan(sinh ξ);k′ = jv.

Ausgehend von der Zusammenfassung

v= F[arctan(sinhξ);k′] = F(θ;k′), θ = am (v;k′), sn(v;k′) = sinθ

ist JACOBI’s imaginäre Transformation für den elliptischen Sinus nun auf direktem Wege zu gewinnen [Jac29, § 19].

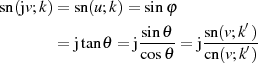
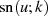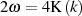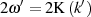Interessant ist daran vor allem zu erkennen, daß $sn(u;k)$ zusätzlich zur reellen Periode $2ω = 4K (k)$ auch eine imaginäre Periode von $2ω ′ = 2K (k′)$ besitzt, d. h. es handelt sich um eine doppelt-periodische Funktion mit dem Periodenpaar $(4K, 2K′)$ .

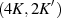Eine ähnliche Transformationsbeziehung kann man mit Hilfe der Verschiebungsrelation 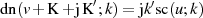$dn(v+ K +jK ′;k) = jk′sc(u;k)$ angeben (siehe Tabelle 3).

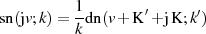
sn(jv;k) = 1dn(v+ K ′+jK;k′) k

Offensichtlich hat 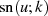$sn(u;k)$ imaginäre Pole 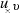$u×υ$ , die genau dort liegen wo 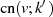$′ cn(v;k)$ verschwindet.¹⁵

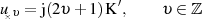u×υ = j(2υ + 1)K ′, υ ∈ ℤ

(58)

Für $cn$ ist diese Transformation ausgehend von Gleichung 31 recht schnell abzuleiten.

Gleichermaßen für die elliptische Delta-Amplitude 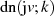$dn(jv;k)$ .

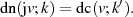′ dn(jv;k) = dc(v;k ).

(60)

Beweis. Ausgehend von der Definitionsgleichung 32 für 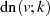$dn (v;k)$ gilt:

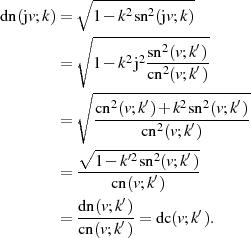
Abschließend noch (ohne Beweis) die anderen elliptischen Funktionen für imaginäre Argumente.

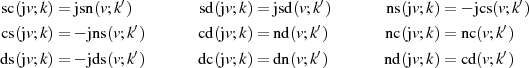
Bemerkenswert ist, daß alle JACOBI’schen elliptischen Funktionen sowohl für imaginäre als auch reelle Argumente immer periodisch sind.¹⁶