


E. I. SOLOTAREff hat sich in [Sol32] mit mehreren praktischen Problemen der gleichmäßigen bzw.
TSCHEBYSCHEff-Approximation auseinandergesetzt, von denen insbesondere das dritte Problem hier von
Interesse sei.62
Es widmet sich der Suche nach einer gebrochen rationalen Funktion 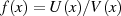 , welche im
Intervall
, welche im
Intervall 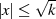 am wenigsten von Null abweicht (mit
am wenigsten von Null abweicht (mit 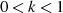 ), dagegen für
), dagegen für 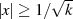 am
stärksten von Null verschieden ist. Dabei sollen
am
stärksten von Null verschieden ist. Dabei sollen 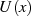 und
und  algebraische Polynome der
Form
algebraische Polynome der
Form
sein, deren Koeffizienten 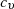 und
und 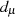 bzw. Nullstellen der Linearfaktordarstellung entsprechend der
Zielvorgabe (für die Fehlerfunktion, vgl. Toleranzschema in Abbildung 21)
bzw. Nullstellen der Linearfaktordarstellung entsprechend der
Zielvorgabe (für die Fehlerfunktion, vgl. Toleranzschema in Abbildung 21)
 | (177) |
bestimmt werden.
SOLOTAREff hat nun aus Symmetrieeigenschaften sowie der Bedingung

die folgende Form von 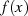 geschlußfolgert [Tod84]:
geschlußfolgert [Tod84]:
 | (178) |
Die Lösung dieser Approximationsaufgabe bzw. der nach 177 beruht auf JACOBI’schen elliptischen Funktionen in Verbindung mit der ersten elliptischen Haupttransformation. Um den speziellen Intervallgrenzen in SOLOTAREff’s drittem Problem Rechnung zu tragen, müssen die Achsen allerdings noch passend skaliert werden. Dazu setzt man in den rationalen Transformationsbeziehungen 140 und 125

und erhält
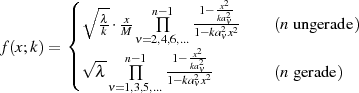
bzw. nach den Parameterdarstellungen 124 und 139 der ersten elliptischen Haupttransformation:
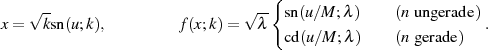
Die Verschiebung der ehemaligen Extremwerte 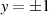 und
und  hin zu
hin zu 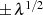 und
und
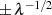 entspricht dem Toleranzschema nach Abbildung 21, wenn man die Verläufe
der ersten elliptischen Haupttransformation in den zugehörigen Abbildungen 15 und 17
betrachtet.
entspricht dem Toleranzschema nach Abbildung 21, wenn man die Verläufe
der ersten elliptischen Haupttransformation in den zugehörigen Abbildungen 15 und 17
betrachtet.
Passt man auch die Berechnungsformeln 138 und 146 für 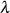 an, dann ist auch
an, dann ist auch 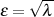 leicht zu
ermitteln.
leicht zu
ermitteln.
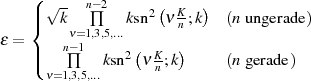
Berücksichtigt man für den Fall eines ungeraden  die Gleichung 136 und für gerades
die Gleichung 136 und für gerades  entsprechend 146 in der Form
entsprechend 146 in der Form
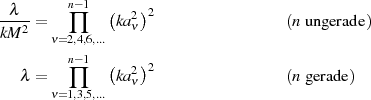
dann ergeben sich noch die folgenden Vereinfachungen:
Bezüglich des SOLOTAREff’schen Ausgangspunktes nach Beziehung 178 kann man nun die
Unbestimmten 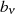 angeben.
angeben.
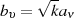
Wegen der Skalierung der x-Achse verschieben sich natürlich auch alle Nullstellen und Pole nach den
Formeln 128 und 127 ( ungerade) sowie 141 und 142 (
ungerade) sowie 141 und 142 ( gerade).
gerade).
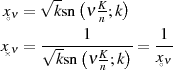
Die Berechnungsformeln 126 und 141 für die Koeffizienten 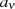 bleiben unverändert bei:
bleiben unverändert bei:
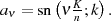
Sie repräsentieren letztlich das Ergebnis der Bestapproximation.
Beweis. Der Beweis der Bestapproximation beruht auf TSCHEBYSCHEff’s Alternantensatz [Mei64, Satz 23], welcher angewandt auf die Ausgangspolynome 176 in kurzer Form lautet [Mei64, § 6]:
Die Funktion 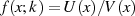 stellt dann eine Minimallösung dar, wenn die absolute
Fehlerfunktion
stellt dann eine Minimallösung dar, wenn die absolute
Fehlerfunktion
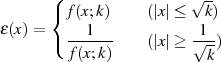
im Approximationsintervall genau 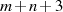 Extremalpunkte hat,63
an denen sie alternierend den Wert
Extremalpunkte hat,63
an denen sie alternierend den Wert 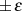 annimmt. Berücksichtigt man den Polynomgrad in
Zähler und Nenner der Lösungsformel 179, dann gilt:
annimmt. Berücksichtigt man den Polynomgrad in
Zähler und Nenner der Lösungsformel 179, dann gilt:
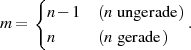
Betrachtet man nun einfach die Funktionsverläufe der ersten elliptischen Haupttransformation in
den Abbildungen 15 und 17, dann ist zu erkennen, daß 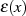 genau
genau  Alternantenpunkte
im Intervall
Alternantenpunkte
im Intervall 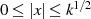 und dazu nocheinmal
und dazu nocheinmal  solcher Punkte im Intervall
solcher Punkte im Intervall
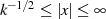 hat.
hat.
Aufgrund ihrer Anzahl sowie des alternierenden Fehlers 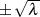 an den Stellen
an den Stellen
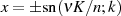 ist die TSCHEBYSCHEff’sche Alternantenbedingung erfüllt und die
Funktion
ist die TSCHEBYSCHEff’sche Alternantenbedingung erfüllt und die
Funktion 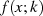 stellt folgerichtig eine Bestapproximation dar. __
stellt folgerichtig eine Bestapproximation dar. __