


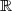
Elliptische Kurven 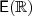 werden in der Normalform nach WEIERSTRASS durch Gleichungen der
Form
werden in der Normalform nach WEIERSTRASS durch Gleichungen der
Form
 | (3.6) |
beschrieben. Wegen der (nur) zwei freien Parameter  und
und 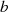 ist jede elliptische Kurve durch zwei
Punkte
ist jede elliptische Kurve durch zwei
Punkte 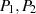 eindeutig definiert. Insofern ist jeder weitere Punkt durch die Kenntnis von
eindeutig definiert. Insofern ist jeder weitere Punkt durch die Kenntnis von 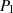 und
und 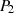 festgelegt.
festgelegt.
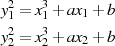
Für  ergibt die Differenz beider Gleichungen
ergibt die Differenz beider Gleichungen
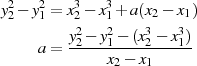
was dann zur Berechnung von 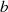 verwendet werden kann.
verwendet werden kann.
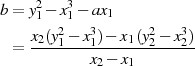
Zieht man entsprechend Abbildung 3.3) durch 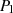 und
und 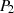 eine Gerade, so berechnet sich ein dritter
(Schnitt-) Punkt
eine Gerade, so berechnet sich ein dritter
(Schnitt-) Punkt 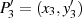 nach der Geradengleichung:
nach der Geradengleichung:
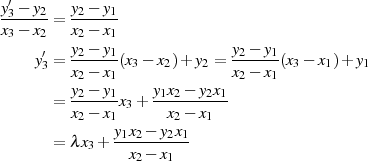
mit dem Anstieg:
Den Schnittpunkt 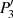 mit der elliptischen Kurve
mit der elliptischen Kurve
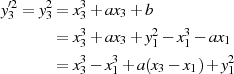
findet man (unter Zuhilfenahme von 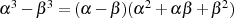 ) durch Gleichsetzen:
) durch Gleichsetzen:
Aus der Geradengleichung ist nun 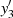 berechenbar:
berechenbar:
und so für den Kurvenpunkt 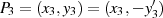 :
:
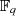
Der kryptographische Anwendungsfall sind elliptische Kurven über endlichen (Restklassen-)
Körpern 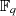 , welche selbst entweder Primzahlenkörper
, welche selbst entweder Primzahlenkörper 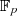 oder auch Binärkörper
oder auch Binärkörper 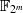 sind.40
Dafür definiert man die Addition zweier Punkte
sind.40
Dafür definiert man die Addition zweier Punkte 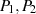 zu
zu 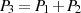 so, daß
so, daß 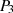 (wie in
Abbildung 3.3 dargestellt) wieder auf der elliptischen Kurve liegt. Die Menge aller dieser Punkte
(wie in
Abbildung 3.3 dargestellt) wieder auf der elliptischen Kurve liegt. Die Menge aller dieser Punkte 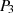 soll eine ABELsche Gruppe
soll eine ABELsche Gruppe 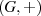 bilden, d. h. es müssen folgende Bedingungen erfüllt
sein:
bilden, d. h. es müssen folgende Bedingungen erfüllt
sein:
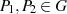 führt zu
führt zu 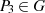 . Für die Kurve
. Für die Kurve 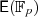 ergeben sich folgende
Formeln:41
ergeben sich folgende
Formeln:41
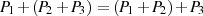 für
für 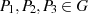 .
.
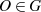 mit
mit 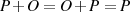 für
für 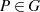 . Nimmt man an, daß
. Nimmt man an, daß
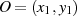 ist, dann muß die Forderung
ist, dann muß die Forderung 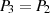 gestellt werden, um
gestellt werden, um 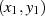 zu ermitteln.
Dazu verwendet man
zu ermitteln.
Dazu verwendet man 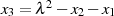 mit
mit 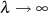 , was zu
, was zu 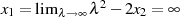 und
und
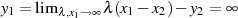 führt. Das neutrale Element ist somit
führt. Das neutrale Element ist somit 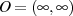 , was
auch geometrisch einleuchtet.
, was
auch geometrisch einleuchtet.
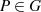 findet man
findet man 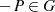 , so daß wieder
, so daß wieder 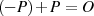 gilt.
Als Folge der Betrachtungen zum neutralen Element (siehe voriger Punkt) ergibt sich:
gilt.
Als Folge der Betrachtungen zum neutralen Element (siehe voriger Punkt) ergibt sich:
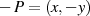
Elliptische Kurven über 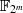 verwenden die Form
verwenden die Form 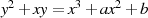 , funktionieren aber
grundsätzlich nach demselben Prinzip. Ohne weiteren Beweis sei hier angegeben (vgl. zum
Beispiel [HMV04, 3.1.2], zu den Algorithmen siehe auch [HHM00, BHHM01, FHLM04, Ano07]):
, funktionieren aber
grundsätzlich nach demselben Prinzip. Ohne weiteren Beweis sei hier angegeben (vgl. zum
Beispiel [HMV04, 3.1.2], zu den Algorithmen siehe auch [HHM00, BHHM01, FHLM04, Ano07]):
![P3 = P1+ P2 = (λ2 +λ + x1+ x2+ a,λ[x1+ x3]+ x3+ y1)](crypto421x.png)
![2 2
P3 = 2P = (λ +λ + a,x + x3[λ + 1])](crypto422x.png) , mit
, mit 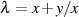
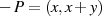
Zur Verifikation eines Kurvenpunktes substituiert man 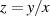 und erhält eine quadratische Gleichung in
und erhält eine quadratische Gleichung in
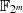 .42
.42
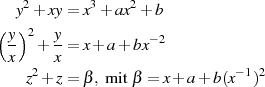
Die beiden Lösungen sind wegen 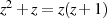 dann
dann  und
und 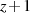 , unterscheiden sich also nur im
niederwertigsten Bit [IEE00, A.12.9].
, unterscheiden sich also nur im
niederwertigsten Bit [IEE00, A.12.9].
Für die kryptographische Anwendung, insbesondere für Verfahren, die auf dem diskreten Algorithmus
basieren, wird zuerst die Gruppenpotenz definiert zu 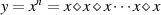 . Das diskrete
Logarithmus Problem besteht nun bekanntermaßen darin die Zahl
. Das diskrete
Logarithmus Problem besteht nun bekanntermaßen darin die Zahl  zu finden, was bei einer
Gruppenaddition per elliptischer Kurve ziemlich schwierig ist. Eines der bekanntesten Beispiele ist die
Umsetzung des Diffie-Hellman Schlüsselaustausches (vgl. Abschnitt 3.2) auf elliptische
Kurven [Ros99]. Aber auch Signatur- und Public-Key Verfahren können damit realisiert
werden [IEE04], [ANS05].
zu finden, was bei einer
Gruppenaddition per elliptischer Kurve ziemlich schwierig ist. Eines der bekanntesten Beispiele ist die
Umsetzung des Diffie-Hellman Schlüsselaustausches (vgl. Abschnitt 3.2) auf elliptische
Kurven [Ros99]. Aber auch Signatur- und Public-Key Verfahren können damit realisiert
werden [IEE04], [ANS05].